さて、気温とビールの売上本数の様な2つのデータの相関関係を数値で表す相関係数を求める時に “共分散” が登場します。
“分散” は知ってるけど “共分散” って何?ってことになります。
“分散” は知ってるけど “共分散” って何?ってことになります。
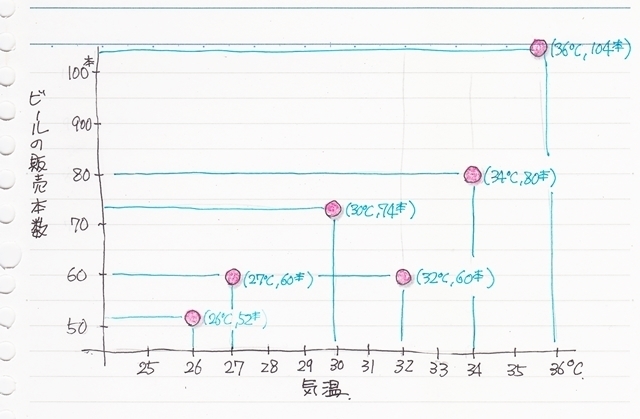
まず、ばらつきはあるもののデータが右上がりに分布しているようです。
と、言うことは。。
・気温が高い時は、ビールの販売本数も多くなる。
もうちょっと推測してみると、気温が平均値より高い時(暑い時)はビールの販売本数も平均値より多くなる。
・と言うことは、気温が平均値より低い時(涼しい時)はビールの販売本数も平均値より少なくなる。
また、縦軸のビールの販売本数を、1本毎じゃなくて、6本パックのパック数で数えると、縦軸の数は1/6に少なるなるけど、それは見かけの数字が少なるなるだけで、両社の関係は何も変わらない。
と、言うことは。。
・気温が高い時は、ビールの販売本数も多くなる。
もうちょっと推測してみると、気温が平均値より高い時(暑い時)はビールの販売本数も平均値より多くなる。
・と言うことは、気温が平均値より低い時(涼しい時)はビールの販売本数も平均値より少なくなる。
また、縦軸のビールの販売本数を、1本毎じゃなくて、6本パックのパック数で数えると、縦軸の数は1/6に少なるなるけど、それは見かけの数字が少なるなるだけで、両社の関係は何も変わらない。
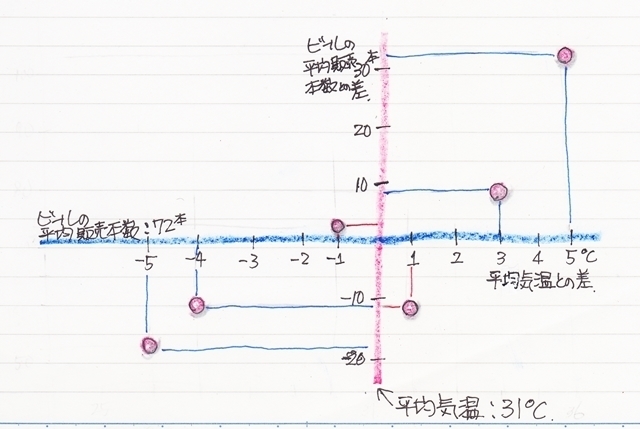
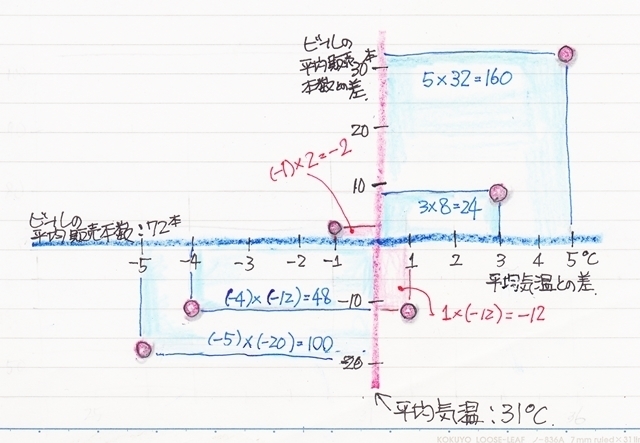
で、ここでこの散布図に気温とビールの販売数の平均値のラインを書き加えてその差を目盛りにしてみます。
すると、なるほど先ほどの推測はほぼそうなっているのが分かります。
右上のエリアと左下のエリアは平均値に対しては真逆の状態なのですが、気温とビールの本数の関係に関しては右上がりと言う同じ状態を表しています
右上のエリアと左下のエリアは平均値に対しては真逆の状態なのですが、気温とビールの本数の関係に関しては右上がりと言う同じ状態を表しています
それではここいらで、共分散の定義はどうなっているか確認してみましょう。
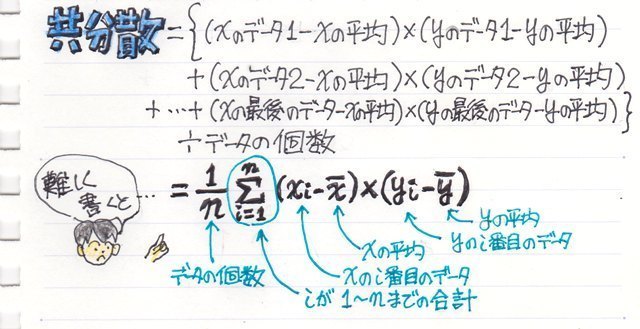
共分散とは 2種類のデータ(2変量)の偏差の積の平均
変量と言うのは、独立して異なる値を取り得る量のことでここでは、気温とビールの本数のことになります。
偏差と言うのはばらつきのことで(データの値-データの平均値)で計算されます。なので平均値より小さい値の場合は符号はマイナスになります。
偏差の積はつまり(気温1-平均気温)x(ビールの販売本数1-平均本数)のことになり
それらをデータ分合計してデータの個数で割った平均値が共分散ということになります。
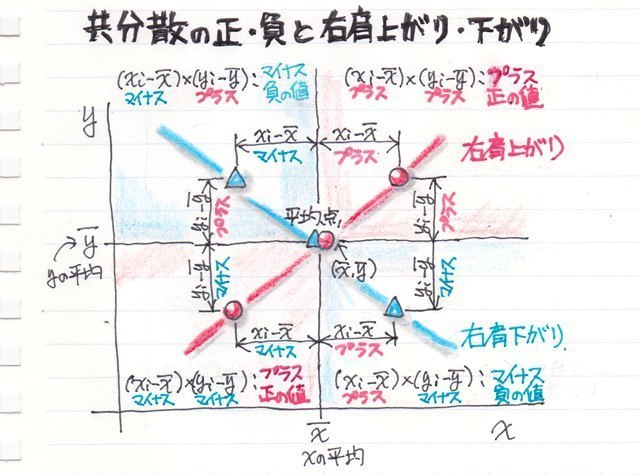
共分散のキモはこの偏差を掛け算しているところです。
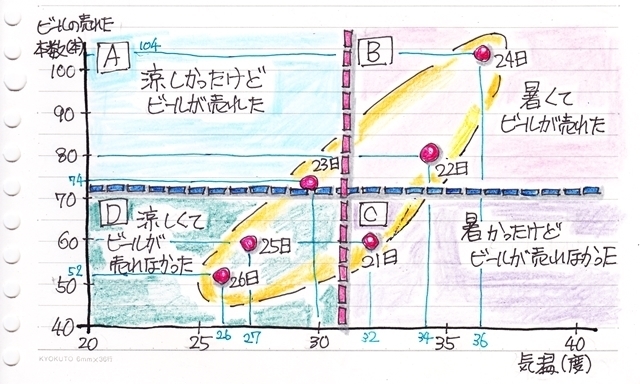
どういうことかと言うと平均値で分割された4つのエリアの偏差の積は[B]と[D]のエリアはプラス(正の値)になると言うことです。
[B]はそれぞれ平均値より上なのでプラスxプラスでプラスの値になり、
[D]もマイナスxマイナスでプラスの値になります。
方や、[A]、[C]のエリアはプラスとマイナスの掛け算になって結果はマイナスの値になります。
[D]もマイナスxマイナスでプラスの値になります。
方や、[A]、[C]のエリアはプラスとマイナスの掛け算になって結果はマイナスの値になります。
で、その偏差積の平均と言うことはまずそれらを足していきます。
偏差積は平均値で出来た軸を基準にした長方形の面積になります。ただ、[A]、[C]のエリアは負の値になりますので、面積に例えるのは間違ってますけどね。
でそれらの平均値ですから、結果正の値なら右上がり、つまり気温が上がるとビールの販売本数が増える(気温が下がるとビールの販売本数が減る)
負の値なら右下がり、気温が上がるとビールの販売本数が減る(気温が下がるとビールの販売本数が増える)と言うことになります。
負の値なら右下がり、気温が上がるとビールの販売本数が減る(気温が下がるとビールの販売本数が増える)と言うことになります。
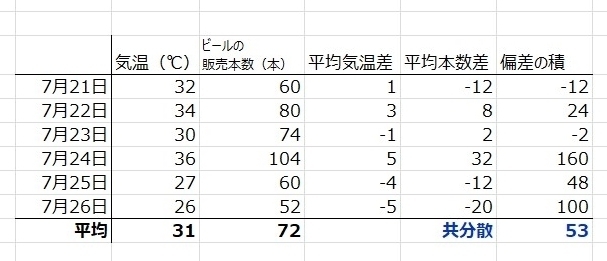
今回の気温とビールの販売本数のサンプルを実際に計算してみると。。
共分散の値は“53”となりました。
この“53”の意味ですが、特にありません。単位は “℃・本” って何それっ!?って意味不明の値です。
なので、この “共分散” 単体で相関関係のどんな特性を表してるかと言うと。。正の値か負の値かだけが特性を表しているだけです。
この値は共分散の値の大きさはビールの本数の単位が変わったり、大きなデータがあると大きく変わるので、共分散の値の大小と2つのデータの関係性は何も関連がありません。
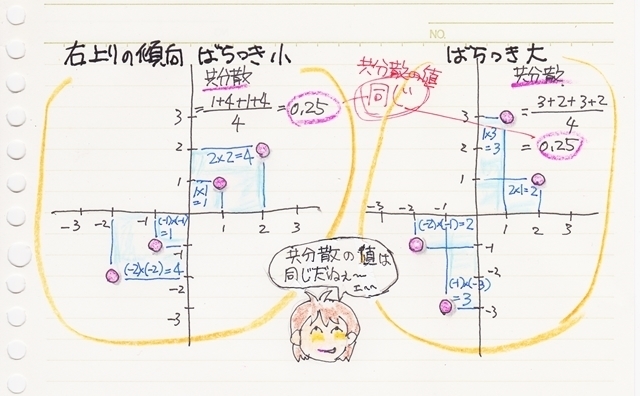
また、“分散”という文字があるので右上がりの直線に対するばらつき具合を表しているのかな〜と思うのですが、例えば散布図のばらつき具合と共分散の値をみると、共分散の値が同じでもばらつきが大きかったり小さかったりするので関連がありません。
まとめると、“共分散” 単体は何を表しているかと言うと結局値が正の値なら右上がり、負の値なら右下がりだけです。
関連ページ
いつものキッチンのやかんでお湯を沸かすのではなく小形のストーブでお湯を沸かしてコーヒーを飲んだりカップ麺を食べたら普段と違う味がするはず!
ラベル:共分散
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1adbd88e.53f98759.1adbd88f.4c3fef22/?me_id=1213895&item_id=10012529&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fshugakuso%2Fcabinet%2F06393848%2Fimgrc0065891851.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fshugakuso%2Fcabinet%2F06393848%2Fimgrc0065891851.jpg%3F_ex%3D240x240&s=240x240&t=picttext)


