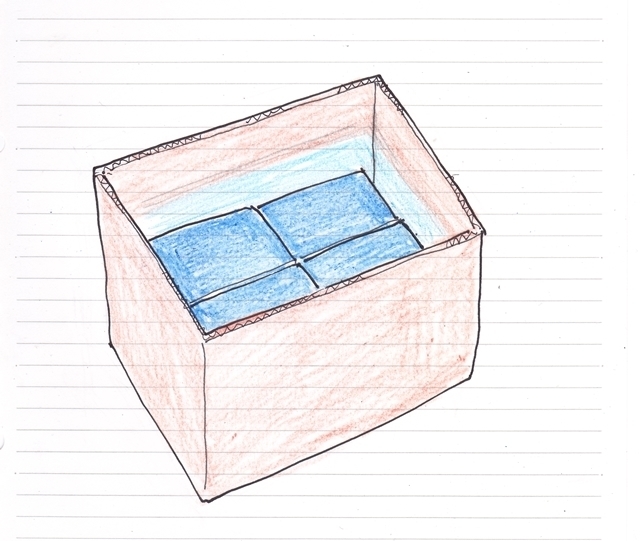
چ«•ï” ‚ة‘خ‚µ‚ؤ“¯‚¶‘ه‚«‚³‚جڈ¬” ‚ً‘S‚ؤ“¯‚¶Œü‚«‚إ” ‹l‚ك‚·‚éڈêچ‡پAڈ¬” ‚جŒü‚«6’ت‚è‚ة‚آ‚¢‚ؤ‚»‚ꂼ‚ê‚جچ«•ïگ”‚ئپA—]‚è‚جƒXƒyپ[ƒX‚ً•\ژ¦‚³‚¹‚ـ‚·پB
—]‚è‚جƒXƒyپ[ƒX‚ً—LŒّٹˆ—p‚µŒü‚«‚ً•د‚¦‚ؤ“ü‚ê‚é‚و‚¤‚بŒvژZ‚ـ‚إ‚ح‚µ‚ؤ‚¢‚ب‚¢‚ج‚إپA‚»‚±‚ح—]‚è‚جƒXƒyپ[ƒX‚ًٹm”F‚µ‚ؤژèŒvژZ‚إ’ا‰ء‚µ‚ؤ‚ف‚ؤ‚‚¾‚³‚¢پB(*پL„DپM)
چ«•ïگ”‚جڈo‚µ•û‚حپAچ«•ï” ‚جٹe•س‚ج’·‚³‚ًڈ¬” ‚ج•س‚ج’·‚³‚إٹ„‚ء‚½ژ‚جٹ„‚èژZ‚جڈ¤پiگ®گ”•”پj‚ئ—]‚èپiڈè—]پj‚ً‹پ‚ك‚ؤڈ¬” ‚ج‘چگ”‚ً‹پ‚ك‚邾‚¯پB
“ء‚ةپA“‚¢‚±‚ئ‚ح‚µ‚ؤ‚ ‚è‚ـ‚¹‚ٌپB‚ھپ[پA” ‚ج•ہ‚וû‚ھ6’ت‚èپA‚إٹi3•س‚جگ”‚ئ—]‚è2‚آ‚جŒvژZ‚ب‚ج‚إپA6×3×2پپ36’ت‚è‚جŒvژZژ®‚ً“ü—ح‚·‚é‚ج‚ھ‚؟‚ئ–ت“|‚إ‚·پB
‚ب‚ج‚إپAƒTƒ“ƒvƒ‹ƒtƒ@ƒCƒ‹پFچ«•ïگ”.xlsx‚ً“Y•t‚µ‚ـ‚µ‚½پB
‚³‚ؤپA
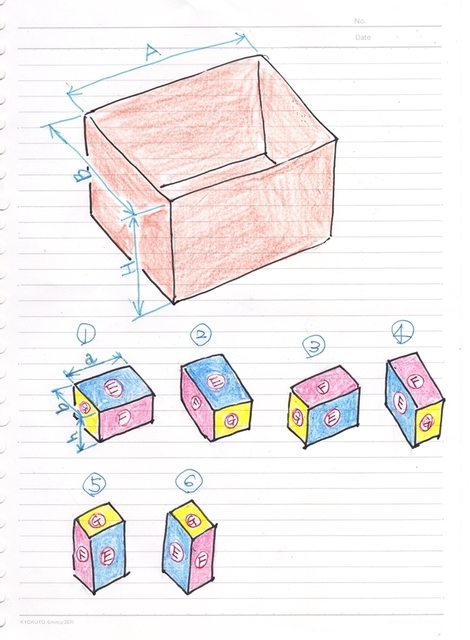
•پFAپA‰œچs‚«پFBپAگ[‚³پFH‚ج’iƒ{پ[ƒ‹” ‚ةپA
•پFaپA‰œچs‚«پFbپAگ[‚³پFh‚جڈ¬” ‚ً
‚»‚ج‚ـ‚ـ‚جŒü‚«‚إ“ü‚ꂽژ‚جگ”‚حپA
••ûŒü‚ة‚ح XaپپA÷a‚جڈ¤پA
‰œچs•ûŒü‚ة‚ح XbپپB÷b‚جڈ¤
گ[‚³•ûŒü‚ة‚ح XhپپH÷h‚جڈ¤
‚ب‚ج‚إپAچ«•ï” ‚ة“ü‚éڈ¤•i‚جگ”‚ح Xa×Xb×Xh ‚ئ‚ب‚è‚ـ‚·‚و‚ثپB
‚إپAڈ¤•i‚جڈ¬” ‚ً“ü‚ê‚éŒü‚«‚ح6’ت‚è‚ ‚é‚ج‚إپA‚»‚ج6’ت‚è‚ة‚آ‚¢‚ؤ“¯—l‚ةŒvژZ‚µ‚ؤ‚¢‚¯‚خ‚¢‚¢‚ي‚¯‚إ‚·پB
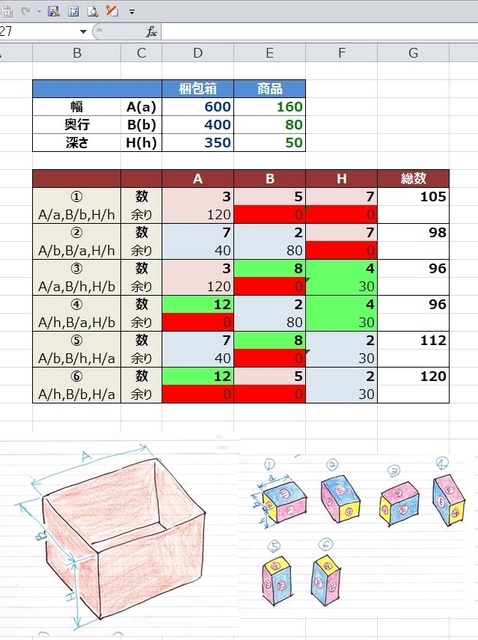
‚إپA‚±‚ٌ‚ب•\‚ًچى‚ء‚ؤ‚ف‚ـ‚µ‚½پB
•\‚ج‰؛‚ة‚حگ}‚ً“\‚è•t‚¯‚ؤ‚ـ‚µ‚½پB‚±‚ê‚ھ‚ب‚¢‚ئ6’ت‚è‚ج•ہ‚וû‚ھ•ھ‚©‚ç‚ب‚¢‚إ‚·‚و‚ثپB
‚±‚ê‚ة‚و‚é‚ئپAچ«•ï” ‚ھ600×400×350‚إپAڈ¤•i‚ھ160×80×50‚جژ‚ة‡E‚ج•ہ‚וû‚جژ‚ةˆê”ش‘½‚¢120Œآ“ü‚è‚ـ‚·پB‚إ‚·‚ھپA••ûŒü‚ئ‰œچs•ûŒü‚ج—]—Tپi—]‚èپj‚حپg0پh‚ة‚ب‚ء‚ؤ‚µ‚ـ‚ء‚ؤ‚¢‚ـ‚·پB
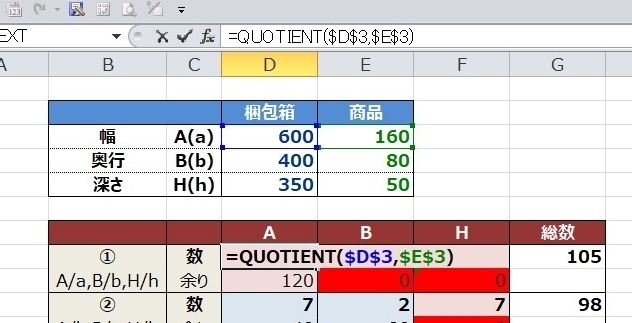
•\‚جگ”‚جŒvژZ‚حٹ„‚èژZ‚جڈ¤‚ً‹پ‚ك‚éپgQUOTIENTپhٹضگ”‚ًژg‚¢‚ـ‚·پB
—]‚è‚حپgMODپhٹضگ”‚ًژg‚¢‚ـ‚·پB
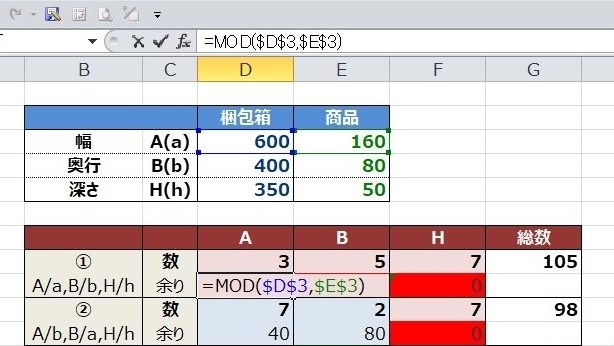
‚ـ‚½پA—]‚è‚ھپg0پh‚جژ‚ح–ع—§‚آ‚و‚¤‚ةƒZƒ‹‚ھگش‚ة‚ب‚é‚و‚¤‚ةڈًŒڈ•t‚«ڈ‘ژ®‚ًگف’肵‚ؤ‚¢‚ـ‚·پB
—]‚è‚ھپg0پh‚ئŒ¾‚¤‚ج‚ح—]—T‚ھ‘S‚‚ب‚¢‚ج‚إژہچغ‚ح“ü‚ê‚ç‚ê‚ـ‚¹‚ٌپB
—]‚è‚ھپg0پh‚ب‚ء‚ؤ‚µ‚ـ‚ء‚½‚çڈ¤•i‚جƒTƒCƒY‚ًژہچغ‚و‚èڈ‚µ‘ه‚«‚‚µ‚ؤ—]—T‚ًژ‚½‚¹‚ؤ‚ ‚°‚ـ‚µ‚ه‚¤پB
ڈ¤•i‚ج‰œچs‚ئگ[‚³‚ً‚»‚ꂼ‚ê2‡o‚¸‚آ‘ه‚«‚‚µ‚ؤ—]—T‚ً‚à‚½‚¹‚é‚ئ‚±‚ج—l‚بŒ‹‰ت‚ة‚ب‚ء‚ؤ‡D‚ج•ہ‚וû‚إ98Œآ“ü‚邱‚ئ‚ة‚ب‚è‚ـ‚·پB
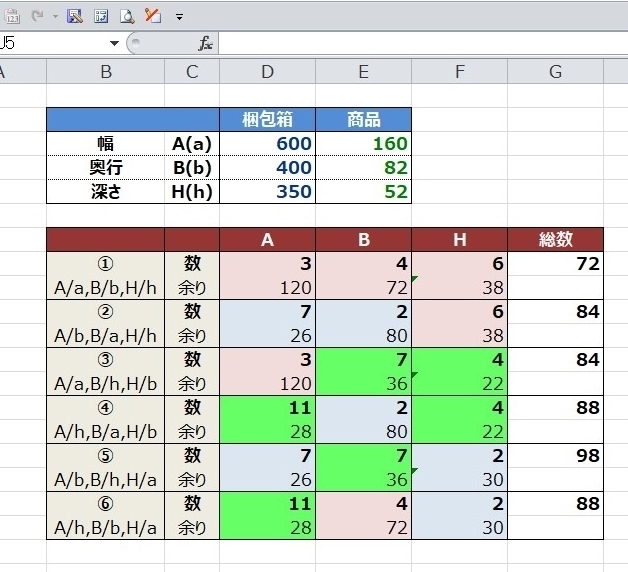 گ}6
گ}6‚ـ‚½پAڈ¤•i‚جڈ¬” ‚ج•ہ‚וû‚حپA•¨‚ة‚و‚ء‚ؤ‚حŒü‚«‚ھگ§Œہ‚³‚ê‚é‚à‚ج‚à‚ ‚邾‚낤‚µپAƒpƒbƒPپ[ƒW‚جŒü‚«‚àگ§Œہ‚³‚ê‚é‚©‚à‚µ‚ê‚ب‚¢‚ج‚إپA6’ت‚è‘S‚ؤ‘I‘ً‚إ‚«‚é‚ئ‚حŒہ‚ç‚ب‚¢‚إ‚µ‚ه‚¤پB
‚ب‚ج‚إ6’ت‚è‚جٹe•س‚جگ”‚ئ—]‚è‚ً•\ژ¦‚³‚¹‚ؤ‚¨‚‚ئŒمپX•ض—ک‚¾‚ئ‚¨‚à‚¢‚ـ‚·پB
ٹضکAƒyپ[ƒW
پEMODٹضگ”‚إٹ„‚èژZ‚ج—]‚èپiڈè—]پj‚ً‹پ‚ك‚ؤ‚ف‚½
‚±‚ب‚¢‚¾ƒzپ[ƒ€ƒZƒ“ƒ^پ[‚ًœpœj‚µ‚ؤ‚½‚çپAƒWƒOƒ]پ[ƒpƒYƒ‹”„‚èڈê‚ج‹ك‚‚ة–طگ»‚ج—§‘ج“I‚ب‘g—§ژ®‚جƒpƒYƒ‹‚ئŒ¾‚¤‚©ƒIƒuƒWƒF‚ھ‚ ‚ء‚½پB
–ت”’‚»‚¤‚¾‚بپ[‚ئژv‚ء‚ؤƒlƒbƒg‚ًœpœj‚µ‚ؤ‚½‚çپA‚±‚ٌ‚ب‚جŒ©‚آ‚¯‚ؤ‚µ‚ـ‚ء‚½پI
—§‘جƒpƒYƒ‹‚ء‚ؤڈ‘‚¢‚ؤ‚ ‚邯‚اپA‚±‚ê‚ح‚à‚¤پA–طگ»‚¨‚à‚؟‚ل‚ج‘g—§ƒLƒbƒg‚إ‚µ‚هپH
‚µ‚©‚àƒSƒ€“®—ح‚إ‘–‚éپI‚·‚²‚¢پI
![[ڈ¤•i‰؟ٹi‚ةٹض‚µ‚ـ‚µ‚ؤ‚حپAƒٹƒ“ƒN‚ھچىگ¬‚³‚ꂽژ“_‚ئŒ»ژ“_‚إڈî•ٌ‚ھ•دچX‚³‚ê‚ؤ‚¢‚éڈêچ‡‚ھ‚²‚´‚¢‚ـ‚·پB] [ڈ¤•i‰؟ٹi‚ةٹض‚µ‚ـ‚µ‚ؤ‚حپAƒٹƒ“ƒN‚ھچىگ¬‚³‚ꂽژ“_‚ئŒ»ژ“_‚إڈî•ٌ‚ھ•دچX‚³‚ê‚ؤ‚¢‚éڈêچ‡‚ھ‚²‚´‚¢‚ـ‚·پB]](https://hbb.afl.rakuten.co.jp/hgb/17e8a884.b7f327f9.17e8a885.f3bcee8f/?me_id=1222178&item_id=10019376&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fsoprano%2Fcabinet%2F06101897%2Fja-70012-1.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fsoprano%2Fcabinet%2F06101897%2Fja-70012-1.jpg%3F_ex%3D240x240&s=240x240&t=picttext)


