二項分布というのは、コインを投げた時の表と裏のような二者択一の場合の確率分布のことで、サンプル数を多くすると正規分布で近似できるという中心極限定理の特殊な場合(特殊中心極限定理?)に当てはまることを数学者アブラーム・ド・モアブルがその著書の中で明らかにしたもので、その計算によって二項分布の計算がとても楽にできるようになったとか?(“二項分布”と“中心極限定理”については各自自習しておいて下さい!?)
ってことで、Excelを使うと二項分布のサンプルは簡単に出来るのでそれが正規分布になるかやってみます。
って言うか、数式で検証するんじゃなくて、Excelでコイン投げを実際にやって正規分布の様になるかグラフを画いてみます。。
コイン投げゲーム
コインを投げた時に、表が“1”、裏が“0”として乱数を発生させてみます。
確率は半々なので50%(0.5)10回連続してコインを投げるた時に表が出る回数の合計は1回も表が出なかった“0”から10回連続で表が出る“10”までの間の値になりますが、“5”になる確率が多くなるというのは想像できるでしょう。。これを確率では"期待値"と言います。
その10回連続コイン投げを200セット行った時、“0”から“10”までの分布をピボットテーブルでヒストグラムにしてみます。
Excelの“RANDBETWEEN関数”で“0”か“1”の乱数を発生させます。それを10(回)x200(セット)で2000個のデータを作ります。
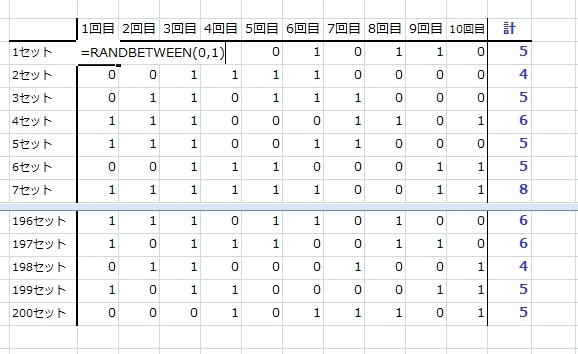
んで、この10回の合計200セットのデータでヒストグラムを作ります。
200セットのうち10回の合計が“5”だった件数が47件、“0”や“10”は1件もありませんでした。。
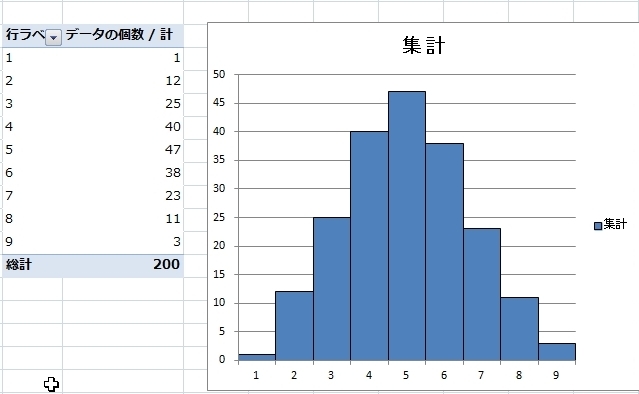
と、正規分布の様に(近似)なりましたよね。。
もしこれが、表("1")が出ると勝ちになるゲームだとして、200人がそのゲームをしたとします。
すると、表が1回しか出なかったまったくツキがなかった人が1人いて、9回も表が出たツキまくった人が3人もいたことになります。
じゃ、10回コインを投げて表が1回しか出なかった人は期待値は5なのだから11回目は絶対表が出るはずだと思って投げました。また、9回表がでたツイてる人は運が向いてるから次も表が出るはずだと思って11回目を投げました。。。さて、2人が投げた11回目のコインは、、、
もちろん1/2の確率で表か裏が出るだけです。こんな感違いって意外にないですか?
確率についてはこちらをご覧ください。
次回は、コイン投げの表が出る確率と正規分布の確率密度について詳しく調べてみましょう!

バックナンバー
正規分布についてまとめてみた
関連ページ
データ分析の解説

