今回は「調和平均」についてみてみしょう。
例えば、自宅から会社ままで自動車通勤をしていて、行きは時速40km/h、帰りは時速60km/hだったとき、平均時速は?
これを、単に算術平均で、
(40+60)÷2=50km/h
でいいかと言うと。。。?
実際に計算してみましょう。
自宅から会社までの距離を30kmとします。
行きにかかった時間は、
30km÷40km/h=0.75h(45分)
帰りにかかった時間は、
30km÷60km/h=0.5h(30分)
なので、
往復の平均時速は、
30x2÷(0.75+0.5)=48km/h
になります。
とこのような時に調和平均 harmonic meanを用います。
調和平均とは、逆数の算術平均の逆数になります。
式で書くとこうなります。
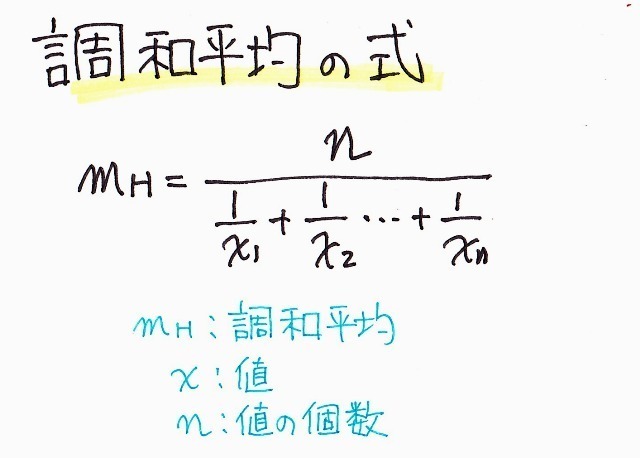
この式で先ほどの例題を解いてみると、
2÷(1÷40+1÷60)=48km/h
になりました!
算術平均と調和平均は間違いやすい時があります。
例えば、車で30分間時速40km/hで走り次の30分を60km/hで走った時の平均速度は?
算術平均の(40+60)÷2=50km/hになります。
最初の30分(0.5h)間で走った距離は40x0.5=20km、
次の30分(0.5h)間で走った距離は60x0.5=30kmなので、
平均時速は(20+30)÷(0.5+0.5)=50km/h
となります。
という訳で、、、
「算術平均」以外の「幾何平均」、「調和平均」についてまとめてみました。
ではいよいよ本題の、統計的に集団の特性を表す平均値以外の代表値の1つである「中央値」について平均値と比較しながらまとめてみました。

バックナンバー
1.平均値と代表値(特性値)
2.算術平均(相加平均)と加重平均の違いは?「重み」ってナニ!?
3.幾何平均(相乗平均)とは?
関連ページ
データ分析の解説/メニュー
算術平均(相加平均)と加重平均の違いは?「重み」ってナニ!?
中央値(median / メジアン)についてまとめてみた


