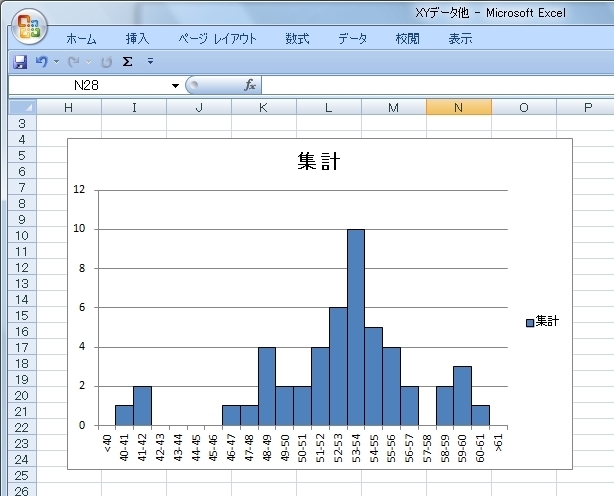
項目別の度数分布ではなく数値データの連続数値に対する度数分布のグラフをヒストグラムと言います。
度数分布表やそれをグラフ化したパレート図は横軸が項目でその項目での度数(データの大きさ)を縦軸に表します。つまり、棒グラフや折れ線グラフで表わすようなデータが対象になります。
それに対し、XYの散布図の様な数値データのばらつきの様子を度数分布で見る場合はどうするかと言うと、横軸をある区間で区切りその範囲に含まれるデータの個数をとって度数として縦軸に表します。
一般的にパレート図の場合は要因分析等の為に使用されるため、度数の多い順に項目が並べ替えられますが、ヒストグラムの場合は横軸が数値軸のためデータの並べ替えはされず、横軸に対する分布を見ることに利用されます。
正規分布データ等がよく知られたヒストグラムになります。
ヒストグラムの形(分布型)をみる
ヒストグラムには分布の形状で、単峰性(山が1つ)と多峰性(山が2つ以上)の大きく2つに分類され、さらに、左右対称かどうか、外れ値があるかどうかなどでの分類がされます。
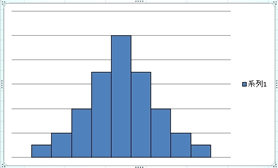
1.単峰性で左右対称
データの集団が同じ種類の場合は、分布するばらつきはその集団の中の個々のばらつきと見なすことが出来、基本的に単峰性左右対称な分布をしまします。この分布が統計的な大原則になります。
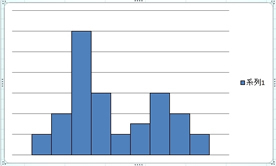
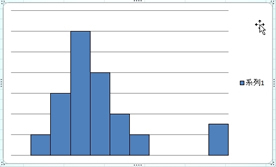
2.多峰性
この様に山が2つ以上あるのを多峰性といいます。
この様な分布の多くは単峰性の分布が2つ重なった場合に見られます。
つまり、測定した集団に異なる別の集団が含まれているような場合になります。
山の高さは、度数の大きさにですから、山の高さが高い方が測定された主な集団になります。
ここから、何の要因で集団が分かれているのかを見つけていく必要があります。
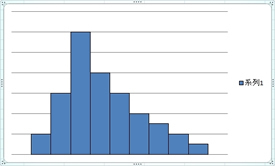
3.非対称(左右対称でない)
山を中心に左右の裾の長さが異なる分布を非対称の分布と言います。図のように、右に裾が長い場合と、左に長い場合があります。
この場合も多峰性の変形と見ることができます。山の高さが大きく異なる多峰性の2つの山を近づけていくとこのような分布に近づきます。
従って、これも異なる集団が隠れていると考え、その要因を見つけます。
4.外れ値
集団から外れたデータがあるものを外れ値といいます。これは、データの入力ミスや誤って他のデータの混入などの場合もあります。
と、このようにヒストグラムをみてその形を分析してみましょう。何かがわかるかも!?
と、このようにヒストグラムをみてその形を分析してみましょう。何かがわかるかも!?
ちなみに、Excelではピボットテーブルを使うと簡単にヒストグラムを作る事ができます。
次回は、多峰性の要因を見つけるヒストグラムの層別にについて解説しましょう。
バックナンバー
統計分析の基本中の基本、度数分布表についてまとめてみた
関連ページ