ある条件(事象B)のもとで、事象Aの起きる確率を"条件付き確率"と言って、P(A∣B)と書きます。
条件(情報)が付くことで確率が変化することを表しています。
その計算式は、、

これを"ベイズの定理"と言います。
簡単な例で説明してみます。(簡単すぎて分かり辛いかも!?)
コインを2回投げた時、
2回の内1回は"表"だった時、もう1回も"表"の確率は、、、
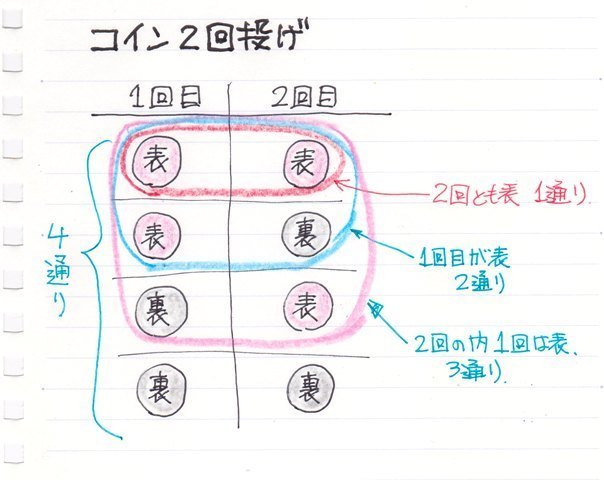
コインを2回投げた時の"表"、"裏"のパターンは全部で4通りだけど、2回の内1回は"表"になるのは3通り。さらにもう1回も"表"になる(2回とも"表")のは1通りなので、
求める確率は1/3になります。
これを、式に当てはめると、、
P(B):2回の内1回は表の確率・・・3/4
P(A∩B):2回とも表の確率・・・1/4
P(A∣B)=(1/4)/(3/4)=1/3
もし、"1回目"が"表"だった時に2回目も"表"になる確率は、、、1/2になります。
つまり、いずれも2回とも"表"になる確率を求めているのだけれど、条件が加わることによって確率が変わってきます。
この条件付き確率(ベイズの定理)は18世紀の牧師さん"トーマス・ベイズ(Thomas Bayes)"によって発見されたのですが、300年の時を経て現代の迷惑メールの振り分け(フィルター)の技術に応用されているとか。。。すごいですねー!
バックナンバー
其の1 確率についてまとめてみた
其の2 標本空間と事象についてまとめてみた
其の3 事象の組合せについてまとめてみた
其の4 期待値についてまとめてみた
関連ページ
データ分析の解説/メニュー

