ある試行を行って、その結果(数値)の平均値のことを言います。
"確率分布の平均"(Mean of probability distribution)ともいいます。

試行の結果の数値をX(χ1,χ2,・・・χn)
それぞれの値の確率をP(p1,p2,・・・pn)
とすると、
期待値 E=χ1p1+χ2p2+・・・χnpn
となります。
例えば、サイコロを1回振った時の出る目を数値として見たときに期待値は、、、
E=1x1/6+2x1/6+3x1/6+4x1/6+5x1/6+6x1/6
=3.5
となります。
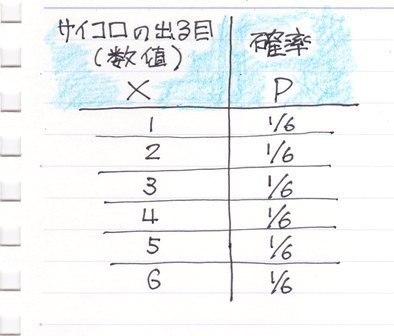
ちなみに、上のXとPの表を"確率分布(表)"といいます。
サイコロを1回振った時の出る目は1〜6まで何が出るか分かりませんが、何回も繰り返していくとその平均は3.5になります。
Excelの関数で"1"〜"6"の乱数を発生させてサイコロ投げ100回をシミュレーションして平均値がいくつになるかやってみましょう。
Excelの"RANDBETWEEN関数"を使用します。
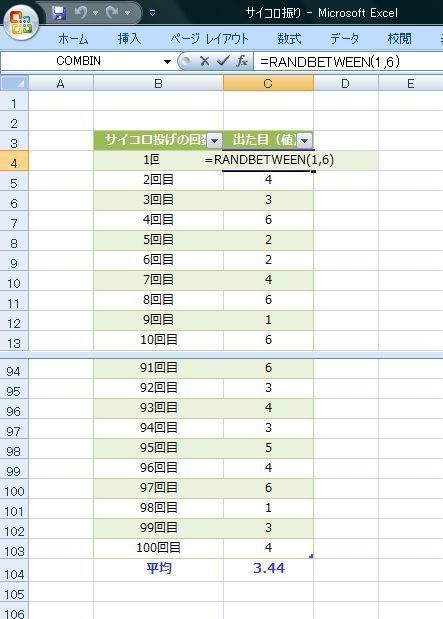
と、100回投げると平均値は"3.44"になりました。
この期待値を求めることで、こんなことが分かります。
サイコロを振って出た目の100倍の金額が当たるくじを企画したとき、1回サイコロを振るくじをいくらにすれば損をせずこのサイコロくじを実施できるでしょうか!?
サイコロの出る目の期待値は3.5なので、このくじの期待値は3.5x100で350円になります。
なので、1回のくじを350円にすればトントン。それより高くすれば儲かります。
くじを引く人はもしかして6を出せば600円当たるかも!と買ってくれるかもしれません。
1しか出なくて100円しか当たらなかった人が次は6を出そうとおもって何回もサイコロを振っても、結果当たりは350円に近付くだけです。。。残念!

と、一見予測不可能なようなことも期待値を計算すれば損得を予測することができるというわけです。
ちなみに、ジャンボ宝くじ(1枚300円)の期待値は150円位なそうなので、悪しからず!?
さて、次回は色々な条件(情報)によって確率が変わる?
現代の迷惑メールの振り分けにも応用されている条件付き確率についてまとめてみました。
バックナンバー
其の1 確率についてまとめてみた
其の2 標本空間と事象についてまとめてみた
其の3 事象の組合せについてまとめてみた
関連ページ
データ分析の解説/メニュー

