ってことで、定義をまとめてみました。

確率とは、
①1つの試行を行った時に、
②n個の場合の内の1つが必ず起こり(同時に2つは起きない)、
③n個の起こる事が同様に確からしく期待でき、
④ある事象がEがn個のうちの特定のr個に限って起きる時、
事象Eの起こる確率は
P(E)=r/n と表す。
というのが確率の定義になります。
もう少し分かりやすく解説すると、、
①「試行」というのは、、、
同じ条件で何度も繰り返すことができて、その結果が偶然によって起きること。
サイコロ振りやコイン投げが試行になります。

②「n個の場合」というのは、、、
試行によって偶然に起こる事の全ての数のこと
サイコロ振りなら6個、コイン投げなら2個になります。
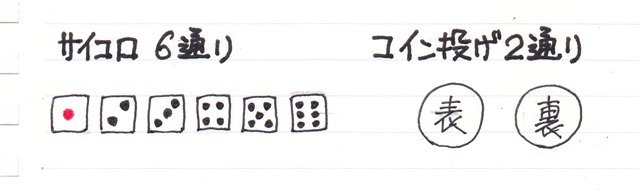
これらは必ず起き、同時に2つは起きません。
偶然起きることを"事象"と言いますが、1番元になる事象を"根元事象"といいます。
③「同様に確からしい」というのは、、、
分かりやすく言うとn個の根元事象が同じ確率で起きるということです。
"確率"の定義で"確率"という言葉はつかえないので、言い換えていると思えばOKです。
確率の式で分母がnになっているのは、n個の起きる確率が同じだからです。
もし違っていたら単純にnで割る事ができませんし、分子も単純にr個にするわけにはいかなくなります。
サイコロなら"1"~"6"全て同じ確率、コインも"表"と"裏"が出るのは同じ確率であることです。
偶数が出やすいいかさまサイコロとか、表が出やすいコインの場合この式に当てはめられません。
④「ある事象E」というのは、、、
n個の根元事象の内のどれかかまたはその組合せ。
例えば、サイコロの目が「"1"か"5"が出る」とか、「偶数の目がでる」とか、
「特定のr個に限って起きる」というのは、、、
事象Eの起きる数が1つになるということです。
例えば、サイコロの目が「"1"か"5"が出る」2個だけの1つ、「偶数の目が出る」のは"2"、"4"、"6"の3個だけの1つということです。
と以上が、P(E)=r/n で表される確率の定義になります。
この定義のをラプラスの定義(先験的定義)と言います。
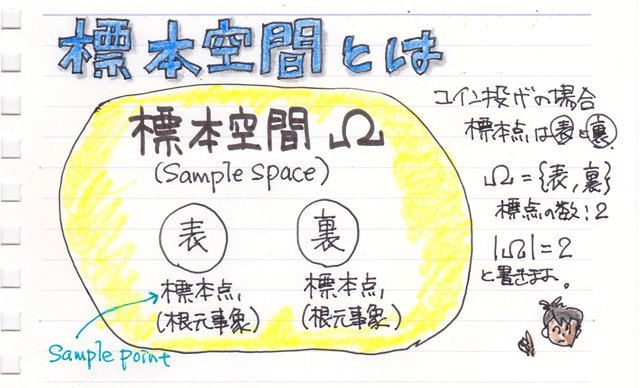
次回は確率を数学的に解いていくために基本的な用語"標本空間"と"事象"についてまとめてみました。
予告編
バックナンバー
関連ページ
データ分析の解説/メニュー

