一般的に、統計調査等を行う場合、全体(母集団)を全て調べるのは、時間も費用もかかり合理的ではないので、全体から無作為(ランダム)に抜取った(抽出した)標本(サンプル)を調査することで、全体(母集団)を予測します。テレビの視聴率とか、世論調査とか。。。身近なところでは、工業製品の検査データ等。。。
ですが、やはり標本の調査結果とそこから推定する母集団の結果には誤差が存在します。この誤差を"標本誤差"(サンプリング誤差:sampling error)と言います。
で、ここで問題になるのがそのような誤差がありながら、標本を調査することにより母集団の値にどれだけ近い推定値を得られるのか、標本から得られたデータの信頼性はどれだけあるのかということです。
そこで、"信頼区間"(Confidence interval)を設けることで、推定値の信頼性をあげます。
例えば、母集団の平均値が"10"の時、標本から得られた平均値が"9.5"だったとします。この時「母集団の平均値は9.5」と推定すると、外れてしまいますが、「母集団の平均値は9〜10」とすれば当たりになって、推定値の信頼性が上がりますよね。。但し忘れていけないのは、母集団の真の値は判っていないということ、つまり標本を調査しても標本誤差は判っていないのです。
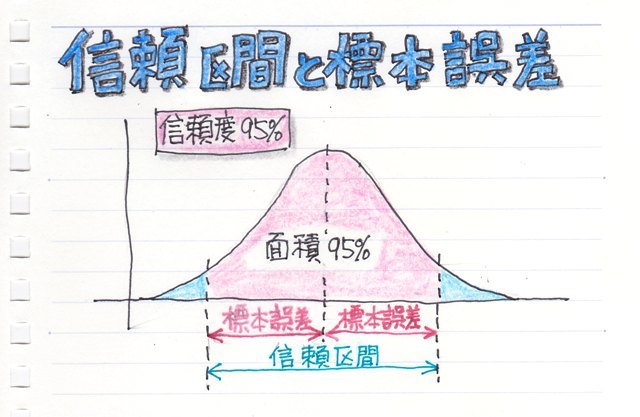
一般的な統計調査では信頼度は95%が用いられますが、さらに信頼度を上げるには信頼区間を広げて標本誤差を大きくしなければなりません。"信頼性を上げる"と言うと"誤差は小さく"なるように勘違いしがちですが、逆です。
機械工学の分野では"許容差"という言葉があって、設計上許容される誤差のことです。不必要に精度の高い部品を作るのは合理的ではないので、予め許容できる誤差を設定しておくことである程度部品がバラついて良し(信頼出来る)とする考え方です。
この信頼性を上げるために信頼区間を広げることも「存在する誤差」を大きくすると考えるよりも「許容できる誤差を与える」ことで信頼性を上げると考えた方がすんなりすると思います。。。
信頼度95%の時の標本誤差は次の式で求められます。

分子はPが"0.5"の時に最大になります。
また分母はnのルートになるので、標本誤差を半分にしたい時は、標本数を4倍にすればいいことになります。
例えば、母集団10,000人のスマホの所持率を調査する場合、100人を抜取って調べた結果40%が所持していたとします。
この時の信頼度95%の標本誤差は、
P=0.4
n=100
を入れると"0.096" 約10%になります。
つまり10,000人のスマホの所持率は30%〜50%という調査結果になります。
標本誤差を半分にするためには400人の抜取って調べなければなりません。
すると、10,000人のスマホの所持率は45%〜55%という結果になります。
ということで、母集団の結果を推定しその標本誤差の妥当性によって標本の大きさを決める必要があります。。。
この"標本誤差"に関しては、国勢調査を実施している総務省や、視聴率を調査しているビデオリサーチのWEBサイト等で詳しく解説が行われています。実際の標本調査では、いかに偏らない"無作為"な標本を抽出するかとか、"非標本誤差"と言って記入ミスや集計ミスなどによる誤差も含まれてきますので、信頼性の高い母集団の推定値を求めることは数式で解決できるほど簡単ではないですね。。。
バックナンバー
其の1 正規分布についてまとめてみた
其の2 確率と正規分布の確率密度についてまとめてみた
関連ページ
・ばらつきと誤差、精度や確度とか
・データ分析の解説/メニュー

