確率についてはコチラで解説しています。。
Excelで、ひたすら10回のコイン投げの表がでるパターンを作ってみます。
表は"1"、裏は"0"で表します。
ちなみに、10回のコイン投げの表が出るパターンは"1024通り"ありますよ!!

んで、表の右下には表が出た回数の平均値を標準偏差を"AVERAGE関数"、"STDEVP関数"で求めておきます。
1通り目が10回とも裏がでるパターン、1024通り目が10回とも表がでるパターンです。
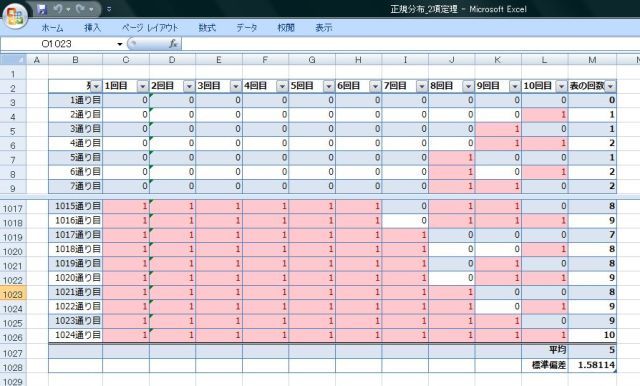
もちろん、コインを投げたときの表と裏がでる確率は50:50なので、10回投げたときの表の出る回数は5回だろうと予測されます。想像通り平均値は"5"になっています。
では、表の出る回数の確率を求めていきましょう。
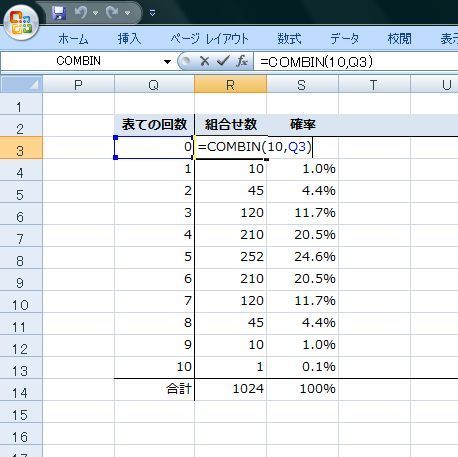
まず、表の出る回数"0回"〜"10回"の組合せの数を求めます。
それぞれの組合せの数を全ての組み合わせ(1024)で割れば確率が求められますよね。
組合せは、こんな式で求められます。

Excelでは"CONBIN関数"で組合せの数を求められます。
投げる回数"10"と、表の回数を指定します。
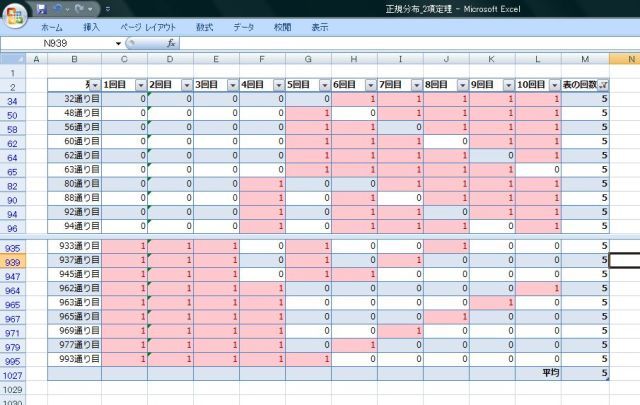
ちなみに、10回投げのパターンの表から"表の回数"を"5"で抽出すると、こんな感じになります。
10回から、5回を抜取る組合せの実際のパターンが分かります。
んで確率は、"COMBIN関数"で求めた組合せの数を、その合計"1024"で割っていきます。
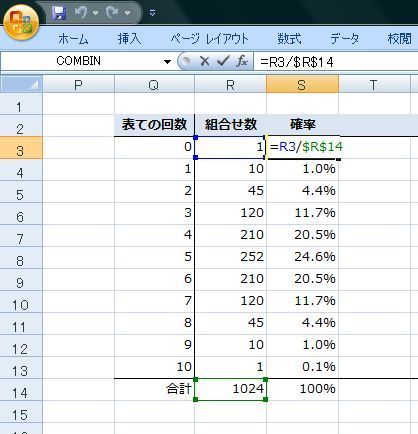
すると、このように、組合せ数とその確率が求められました。
表5回は"252回"、確率は24.6%です。
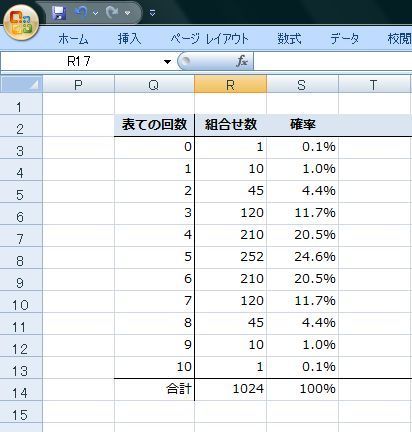
では、次にこの1024通りのデータから、Excelの"NORMDIST関数"を使って正規分布の"確率密度"、"累積分布"を求めてみます。
正規分布は"平均値"と"標準偏差"が分かれば求められます。
さっきの、1024通りの表で求めてあった"平均値:5.0"と"標準偏差:1.58114"を引用します。
確率密度は最後の引数に"FALSE"を指定します。
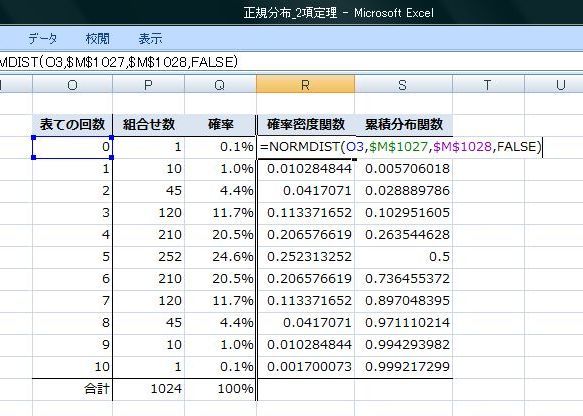
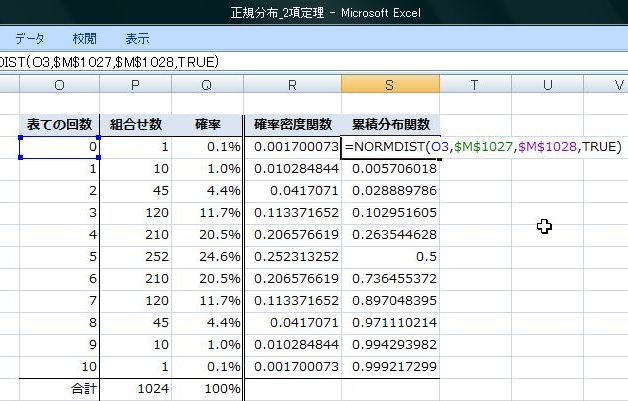
累積分布の最後の引数は"TRUE"です。
つなみに、確率密度関数のグラフ、つまり正規分布のグラフはこうなりました。
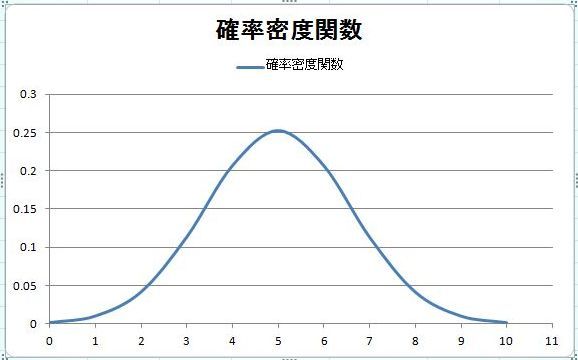
で、確率と比較するとこうなりました。
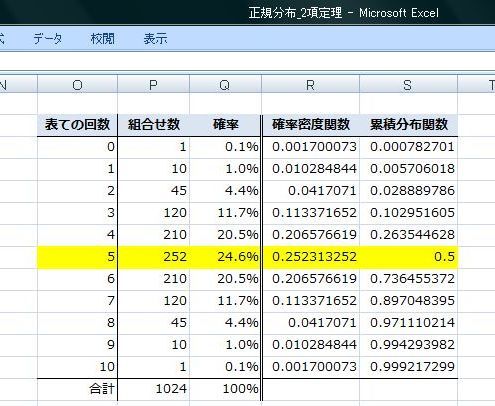
さて、コイン10回投げで表が5回出る確率は"24.6%"ですが、正規分布のベルカーブ曲線の確率密度関数では"0.2523"になっています。
前回も説明しましたが、確率密度とは、単位幅当たりの確率のことで、確率とは異なります。
確率は曲線から下の面積(確率密度を積分したもの)になります。
また、正規分布の横軸の数字は連続した数値です。コイン投げでは表の回数は整数で、4.5回なんてのはあり得ませんが、正規分布はありです。コイン投げのような場合のとる値は"離散的"といい、連続数と区別されます。
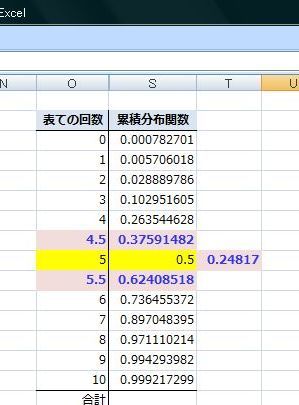
正規分布では面積が確率になるので、総面積が"1"(確率の合計)になるのですが、累積分布関数の"10"の値は"0.999217299"で"1"にはなっていません。
これは、正規分布の横軸は"-∞から∞"であるためです。
累積分布関数で"4.5"と"5.5"の値を求めてその差(確率)を求めてみると"0.248"となり、10回投げで表が5回出る確率とほぼ同じになりました。
んで、前回"RANDBETWEEN関数"を使って10回のコイン投げを200セット行った時の表が5回出た確率"47/200=0.235"はほぼ妥当だと言うことがわかりますね。。
確率を求めてみたところで、もう一つ気になることがあります。
コイン投げの表と裏がでる確率は50:50で、10回投げたら表が5回でるのが予想値なのですが、その予想値が当たる確率は約25%しかないということです。75%は外れてしまうのです。。。
もし、"5±1回"と予想すると、4回〜6回が予想対象となるので、その確率"20.5%"+"24.6%"+"20.5%"="65.6%"が当たります。
次回は、サンプルを抽出して分析する際の"標本誤差"について説明します!
予告編
バックナンバー
其の1 正規分布についてまとめてみた
関連ページ
確率についてまとめてみた
COMBIN関数で組合せ(抜取り)の数を求めてみた
データ分析の解説/メニュー

