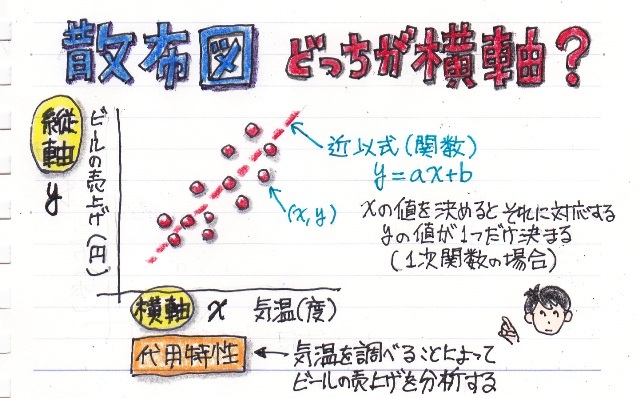
散布図というのは、横軸と縦軸に2つの別の量(数値)をとって、そのデータをグラフ上に点を打った(プロット)グラフです。
そのグラフ上に散らばった点の分布状態から、2つの値の相関関係を見ることが出来るます。
どっちを横軸にしたらいいか?
散布図を作る場合、2つのデータの内、どっちを横軸にしたらいいか、縦軸にしたらいいかという疑問がでてくると思います。
ここで、大切なことは「相関関係を調べる目的は何か?」ということです。
統計的なデータ分析をする目的の一つに、あるデータ変動から別のデータの変動を分析し推定(予測)したりするというのがあります。
例えば、気温とビールの売上の相関関係を調べる目的は?気温の変動からビールの売り上げを分析し、予測するためですよね。ビールの売上を調べて気温を予測することは無いでしょう。。
このような場合、品質管理等では“気温”のことを“代用特性”と言います。つまり、知りたいビールの売上を“気温”で代用させる訳です。
んで、話を戻すと、このこのような代用特性のデータを横軸にします。逆の視点でいうと分析(推定・予測)したい目的のデータを縦軸にとります。
では、算数と理科の成績の相関関係の場合はどうでしょう。なんとなく算数が横軸ですよね?つまり理科には数式が出てきたりするので算数の学力が理科のベースになっていると考えることができます。数学と物理と言った方がもっとはっきりするかもしれません。
算数の成績が最近伸びてきたから、次の理科の試験もきっといい点取れるかもね。。。とか、、
ということで、横軸、縦軸を使い分けましょう。。。
数学的にいうと
数学的には、散布図は“x-yグラフ”と呼ばれる場合もあります。棒グラフや、折れ線グラフなどでは、横軸は数値ではなくラベル(項目)ですが、それに対し、散布図は横軸、縦軸な2つの数値データになり、横軸は“x軸”、縦軸は“y軸”になります。
プロットされるデータはxの値とyの値を持っています。
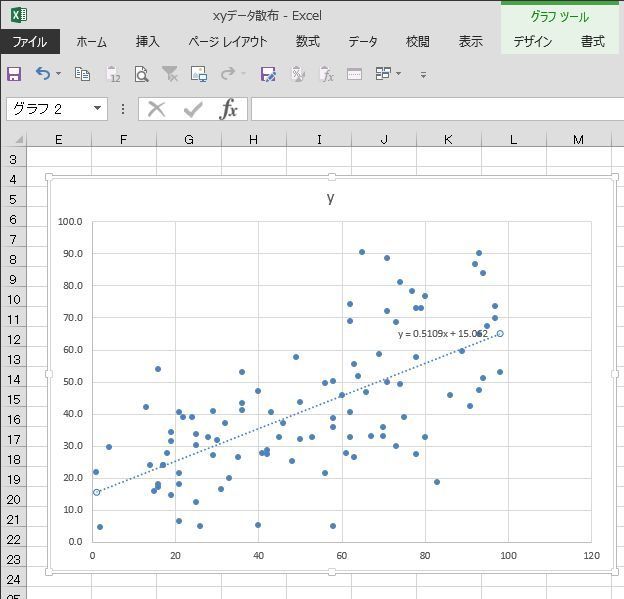
出来上がった散布図から“x”と“y”の関係を y=ax+b 等と数式(関数)で表したりすることも出来ます。(近似式と言います)
上の数式のような1次関数の場合「xの値を決めるとそれに対応するyの値が1つだけ決まる」といいます。
Excelで散布図を作る場合、“x軸”、“y軸”という言葉がいきなり出てきますが、そういうことなんで、ビビる必要は全くありません!
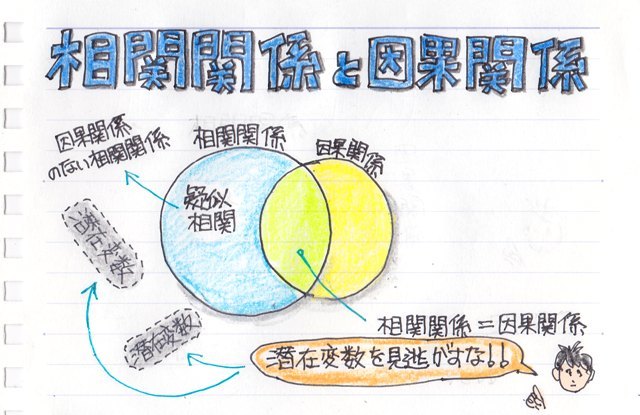
さて次は、その散布図を描いて相関関係と因果関係について簡単にまとめてみました。
予告編
バックナンバー
其の1 相関関係についてまとめてみた
其の2 相関関係で気をつけたいこと(散布図を画いて確認しよう!)
関連ページ
其の4.1 散布図を画いてみた / グラフ
COVAR関数で共分散を求めてみた
CORREL関数で相関係数を求めてみた”
データ分析の解説/メニュー

