相関グラフ(散布図)もちゃんと画いて確認しないと間違いを見落としてしまうケースがあったりします。
今回はそんなことも含めて、相関分析で気をつけておきたいことをまとめてみました。
外れ値
“外れ値”というのは、データの入力ミスだったり、異なるデータが混在したりして、極端に大きい(小さい)データのことで、この外れ値があると“平均値”が大きく変わってしまうことがよく知られています。
相関分析でも、外れ値があると相関係数が小さくなってしまいます。
これを見分けるには相関グラフ(散布図)を画いてみないと見過ごしてしまいます。
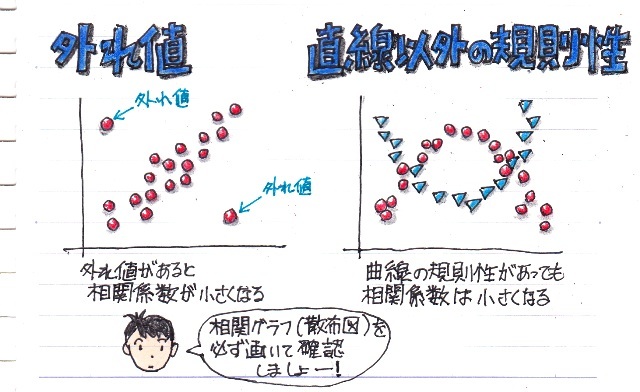
直線以外の規則性
前回も説明したように、相関係数は分布が直線に近似できる場合の相関を表す数値です。
なので、上の図のように曲線の規則性あっても、相関係数では相関が無いような結果になってしまうことがあります。
ので、これも相関グラフ(散布図)を画いてみることが必要です。。
データの混在(層別にする)
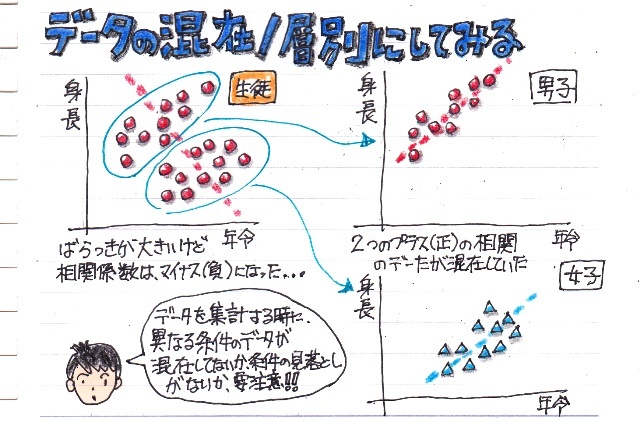
せっかく相関グラフ(散布図)を画いてみても、そのデータに本来別なデータとして扱わなければならないものなのにそれに気づかずに一緒に混ぜてしまい、相関が無くなってしまったり、上の図の例の様に、正負が逆の結果になってしまうこともあります。
対象とするデータに異なる条件が隠れていないか、よく吟味しなければなりません。
これは、そのデータに関する専門的な知識が必要になる場合もあって、ちと大変です。。。
選抜効果
広い範囲に分布する全体のデータは明らかに相関があるんだけど、その中の1部分を取り出すと、相関が小さくなってしまうことを“選抜効果”と呼ばれます。
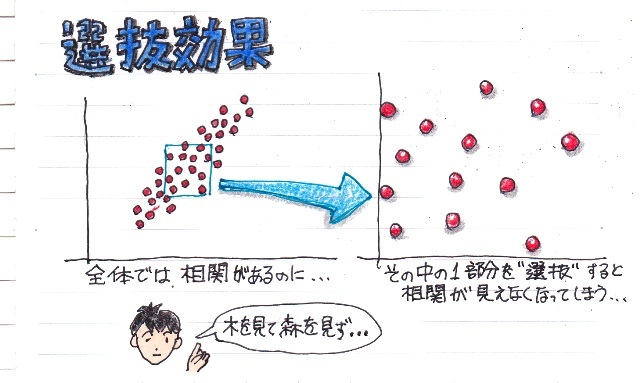
この選抜効果でよく例えに挙げられるのが、入試を行って合格者の、入試の時の得点と、入学後の成績の相関をみると相関が無いという結果になるという話。。。
この場合、“入試で合格した”で範囲を狭く選抜してしまったことが相関を無くしてしまう原因になるわけです。。。
なのだけど、選抜された範囲で相関が弱くなるのは、決して分析が間違っているわけではなくそれはそれで真実な訳です。
つまり、実際に必要とする分析の範囲がどこかによって、相関は変わります。
もし、全体から選抜した範囲の相関を求めたい時は、全体の相関も求めたうえで、選抜した範囲の相関を評価するべきだと思います。。
っと、いう訳で、相関係数だけでは分からないところ、見過ごしてしまうところがあります。
散布図を画けばおぎなえるところ、散布図を画いても分からないこともあります。
データの背景をよく見て(データを収集して、分析して)正しい(妥当な)相関を見つけましょう!!
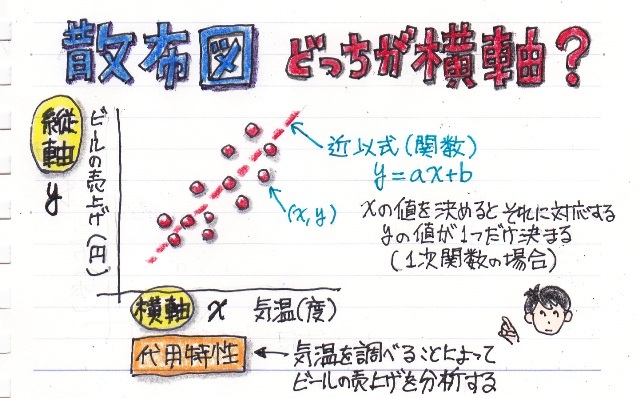
さて次は、その散布図について簡単にまとめてみました。
予告編
バックナンバー
其の1 相関関係についてまとめてみた
関連ページ
其の3 散布図についてまとめてみた(どっちが横軸?)
其の4.1 散布図を画いてみた / グラフ
COVAR関数で共分散を求めてみた
CORREL関数で相関係数を求めてみた”
データ分析の解説/メニュー

