COVAR関数を使用します。
“COVAR”というのは“Covariance”(コヴァリアンス)「共分散」の略です。
共分散は相関関係の相関係数を求めるために使用されます。
相関関係(相関係数・共分散)の解説はこちらをご覧ください。
このような相関グラフ(散布図)があります。(データはサンプルです)
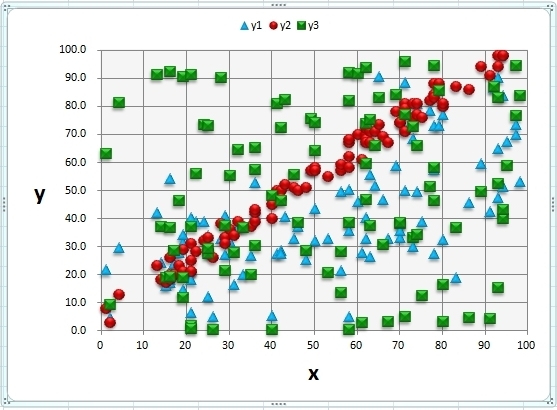
y2(赤○)はばらつきが少なく右肩上がり、
y1(青△)はばらつきのある右肩上がり
y3(緑□)はばらつきが大きく、グラフの傾向もよくわかりませんね。。
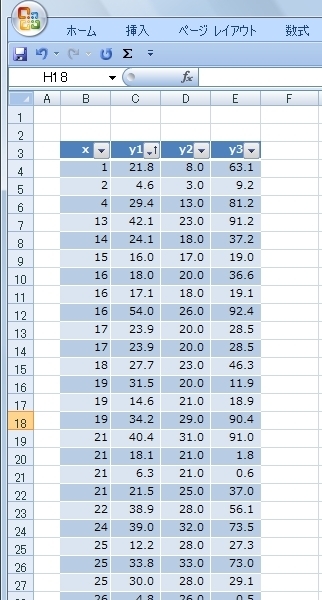
グラフの元データはこんな感じです。
テーブルの設定をしています。
では、早速。
「数式」「その他の関数」「統計」から「COVAR」を選択します。
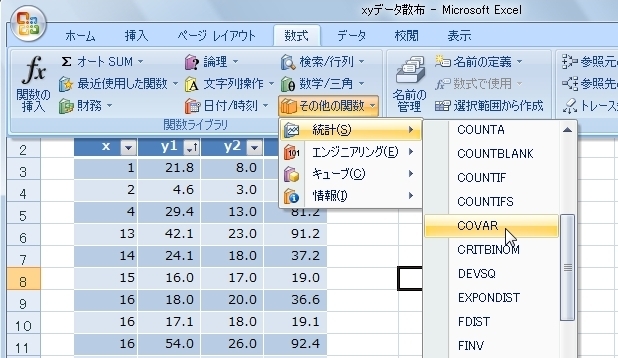
「関数の引数」画面が開きます。
配列1:xの値が入力されているセル範囲を指定します。
配列2:y1の値が入力されているセル範囲を指定します。
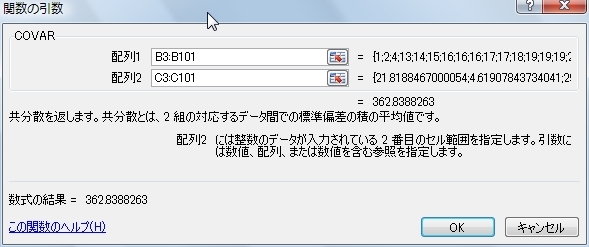
セルの式はこうなります。
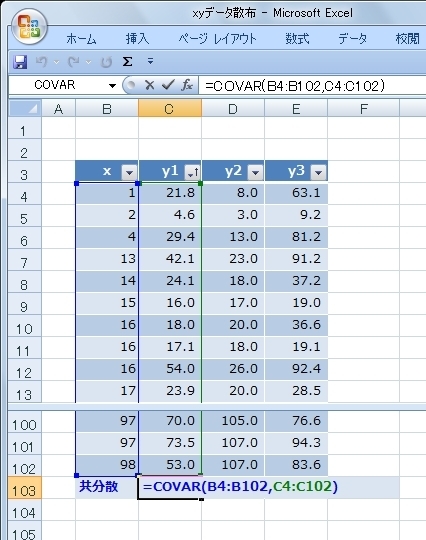
同じように、y2、y3の共分散も求めましょう。
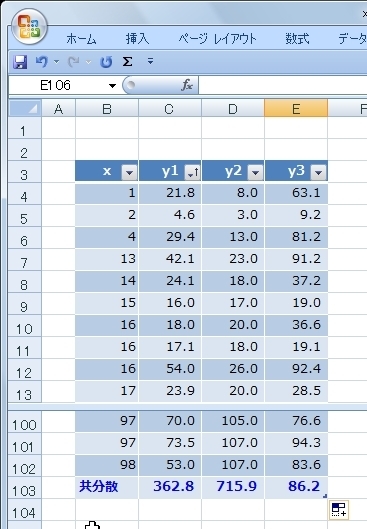
と、このように共分散を求めることができました。
値の大小はあるものの、全てプラス(正の値)になっているの殆ど傾向が見えなかったy3も含めて全て右肩上がりのグラフであることがわかります。
では、共分散を求める数式をつかって計算で求めてみましょう。
解説にもありますが、数式はこうなります。
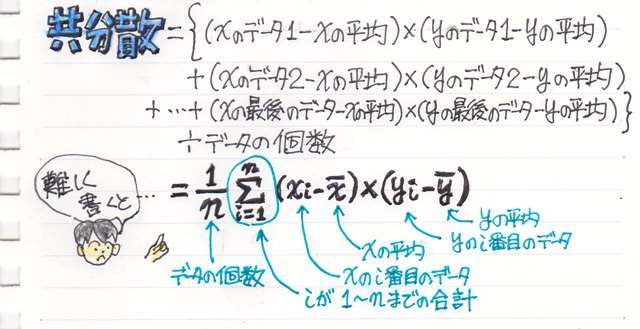
まず、x、y1、y2、y3の平均を“AVERAGE関数”で求めておきます。
それぞれのデータの平均との差(ここでは“平均差”と命名)を求めます。
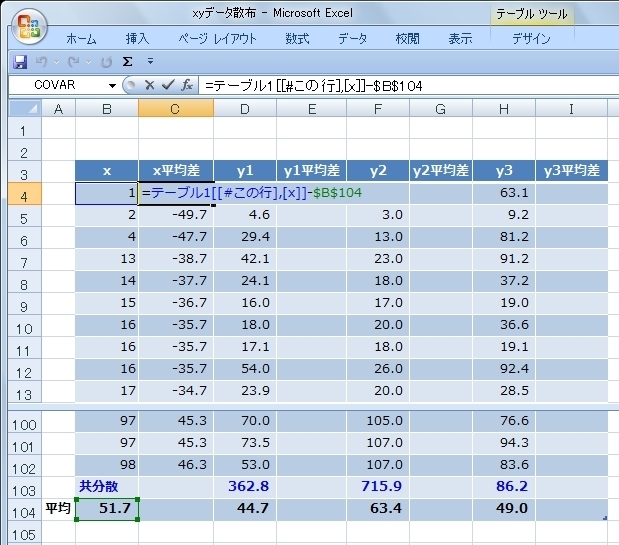
次に、xの平均差と、yのの平均差の積(ここでは“平均差積”と命名)を求めます。
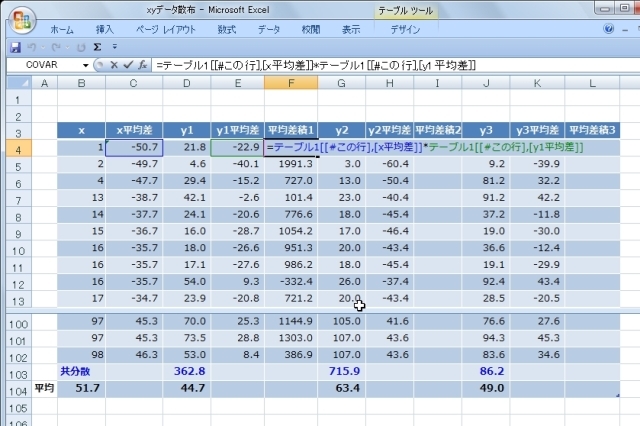
共分散は平均差積の平均なのでここも“AVERAGE関数”で平均をもとめます。
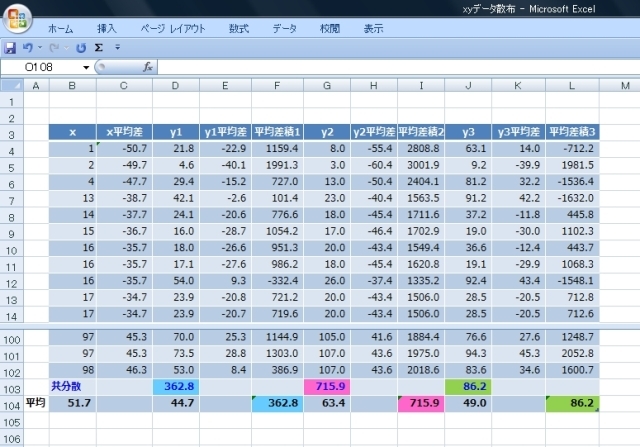
と、“COVAR関数”で求めた共分散と一致しました。
で次は、共分散から相関係数を求めてみましょう。。
関連ページ
相関関係(相関係数・共分散)
関数一覧(カテゴリ別)
関数一覧(名前別)
エラー値について(#VALUE!、#DIV/0!、#NAME?、#N/A、#REF!、#NUM!、#NULL!とか)

