前回は“平均との差”の平均“分散”についてまとめましたが、今回は“標準偏差”について詳しくみてみましょう。
例えば、テストを行った各学生の点数がこんな点数で、平均は63点でした。
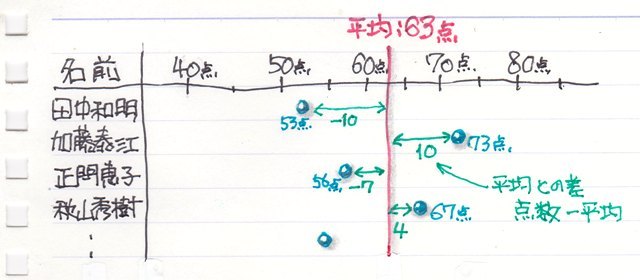
さてここで、加藤さんは73点で平均より10点高かった訳ですが「10点も高かった」と言えるのか、それとも「10点しか高くなかった」としか言えないのか。。。?
テストの結果をヒストグラムにしたとすると、、
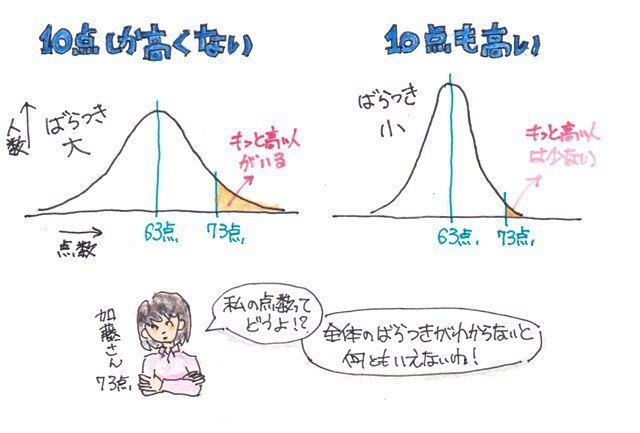
ばらつきが大きかったとすると左のようになだらかな分布になり、ばらつきが小さいと右のような尖がった分布になります。
平均値より10点高かった加藤さんですが全体の分布がどうなっているか(ばらつきが大きいのか小さいのか)によって、全体の中での位置付けが変わってくるわけです。
そのばらつきの大きさを数値で表したのが"標準偏差"(Standard Deviation)です。
分散と標準偏差の求め方
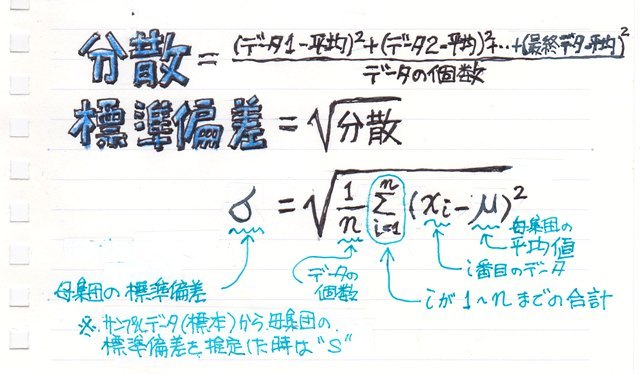
標準偏差を求めるためにまず"分散"(variance)を求めます。
分散は平均との差(点数-平均)の二乗の平均値です。
で、標準偏差はその分散の平方根になるわけです。
平均との差(点数-平均)を単に平均してしまうと、プラス・マイナスで相殺されてしまいます。
例えば田中君の53点と加藤さんの73点の平均との差をそのまま足してしまうと-10+10=0になってばらつきが無くなってしまいます。そこで一旦二乗を平均したのが分散になります。
平均値が同じでも標準偏差が異なるとデータのばらつきが違いますから、データの分布の様子が変わってくるわけです。
よく聞く“正規分布”と言うのは“平均値”と“標準偏差”だけで、分布の形が決まります。
ですが、標準偏差はばらつきの大きさを表しているだけなので、正規分布にはなっていない分布でも用いることができます。
平均との差の平均は、平均との差の絶対値から平均を求める方法もあり、これを“平均偏差”といます。二乗の平均から平方根にした標準偏差とは値が異なります。
一般的に標準偏差は“σ(シグマ)”で表示されますが、これは母集団の標準偏差の場合で、サンプルデータ(標本)から母集団の標準偏差を推定する場合は“s”で表示され、データの個数は"n"ではなく"n-1"になります。
明確に区別する場合は標本(サンプル)の場合は"標本分散(または不偏分散)"、"標本標準分布"が使われます。
Excelの関数では“標本から予測した(母集団の)標準偏差”を求める“STDEV関数”“母集団の標準偏差”を求める“STDEVP関数”が用意されています。
さて標準偏差が分かったところで、次回は色々な種類のデータを比較できる様にするためのデータの標準化についてまとめてみました。

バックナンバー
データの変動と分散についてまとめてみた
関連ページ
・統計分析の基本中の基本、度数分布表についてまとめてみた
・数値データの分布をみるヒストグラムについてまとめてみた
・正規分布について
・平均偏差、ばらつきの平均
・データ分析の解説/メニュー

