�f�[�^����������������ׂ����ɂ��傤�ǐ^�ɂ���l�̂��Ƃł��B

���������ϒl�ł͋ɒ[�ɑ傫���f�[�^��ɒ[�ɏ������f�[�^�i�O��l�j��1�ł�����Ƃ��̒l�ɂ���ĕ��ϒl���傫���ς���Ă��܂��܂��B
�f�[�^�����K���z�ɋ߂��ꍇ�̓f�[�^�̏W�c�̓����ϒl�ő�\������i��\�l�j���Ƃ��ł��܂����A���K���z����O��Ă��܂��Ă���ꍇ�͕��ϒl�ł͏W�c�̓������\������ɂ͓K���ł͂���܂���B
�Ȃ̂ɁA�g���ϒl�h�͘V��j�����킸�L���m��n���Ă��邽�߁A���Ȃ�̊����Ő��K���z����傫���O��Ă��܂��Ă��Ă����̏W�c�̑�\�l�Ɂg���ϒl�h���g���Ă��܂��B
�����l�́A���̂悤�ȏꍇ�ɕ��ϒl�ɑ����ďW�c�̑�\�l�Ƃ��Ďg�p���邱�Ƃ��ł��܂��B
�����l�̋��ߕ�
�f�[�^�̐�����̎��́A�^���ɂ���f�[�^������܂����A�����̎��͐^���̃f�[�^�͂���܂���B
���̎��́A�܂�Ȃ���2�̃f�[�^�̕��ϒl�𒆉��l�Ƃ��܂��B
�Ⴆ�A10�l�̎q����������5�Ԗڂ�6�Ԗڂ̎q���̐g���̕��ϒl�������l�ɂȂ�܂��B
���ŏ����Ƃ����Ȃ�܂��B
���Ȃ݂ɋL���́g�ԁh�̏�Ɂg~�h�i�`���_�L���j�����āg�G�b�N�X�`���_�h�ƌĂт܂��B

�悭�A�X�|�[�c�̍̓_�ő̑��A�t�B�M���A�X�P�[�g��V���N�����̍̓_�ł͍̓_�̍ő�l�ƍŏ��l�������Ă��畽�ς���g�g�������ρi�������ρj�h���̗p����Ă��܂��B����͕��ϒl���O��l�̉e�����₷�����߂ɂ��̂悤�ɂ��Ă���̂ł����A���̃g�������ς̎�菜�������ǂ�ǂ₵�Ă����Ďc�����Ō�̃f�[�^��1�i�܂���2�j�ɂȂ������̒l�������l�Ƃ������ƂɂȂ�܂��B
�����l�ƕ��ϒl���ׂĂ݂��
�O��l�����鎞�͊ԈႢ�Ȃ������l��p����̂��Ó��ł��B
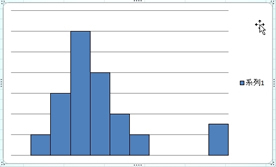
�ł́A���z�����E�Ώ̂ł͂Ȃ����Ă���ꍇ�́H
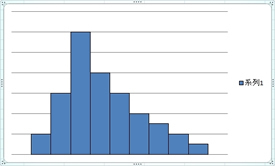
���̏ꍇ�A���ϒl�͖��炩�ɉE���̒l�ɂȂ�܂��B
�悭�A���^�����҂̕��ϒ��������ɍ�����������̂͊ԈႢ�Ȃ����ׂ̈ł��B
�����l���Ƃ��ꂪ�ɘa����āA����ɋ߂��l�ɂȂ�ł��傤�B�������R�̃s�[�N�i�ŕp�l�j���͉E���ɂȂ�܂��B���̏ꍇ�͍ŕp�l���ł������̐l�������ł���l�ɂȂ�܂��B
�Ⴆ�A�e�X�g��������5�l�̐��k�̓_���i�@�`�D�j���A
�@10�_�A�A10�_�A�B30�_�A�C70�_�A�D80�_�������Ƃ��܂��B
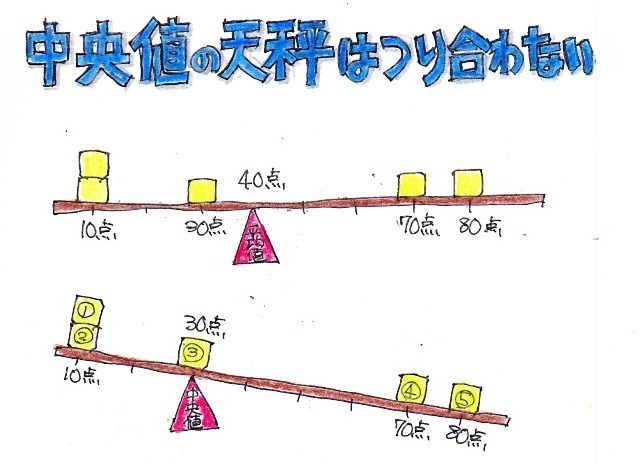
�O��̎Z�p���ςƉ��d���ς̘b�ɏo�Ă����V���̒ނ荇�����l���Ă݂�ƁA
���ϒl�́i10+10+30+70+80)÷5=40�_�ŏd�S�ɂȂ�V���͒ނ荇���܂��B
�����l�͇B�Ԗڂ̒l�A30�_�ɂȂ�V���͒ނ荇���܂���B
�܂�����3�Ԗڂ̏��Ԃ����ς��Ȃ���A���̇@�A�A�A�C�A�D�̓_���������ł��낤�������l�͕ς��܂���B
�Ƃ����킯�ŁA�f�[�^�̑�\�l�Ƃ���"���ϒl"���g����"�����l"��"�ŕp�l"�����Ó����f����ɂ��x�����z�}�i�q�X�g�O�����j���܂�����悤�ɂ��܂��傤�I
Excel�ł́A�����l�����߂�gMEDIAN���h���p�ӂ���Ă��邽�߁A�f�[�^�̐�������������Ƃ����C�ɂ��邱�Ƃ͂���܂����B�B
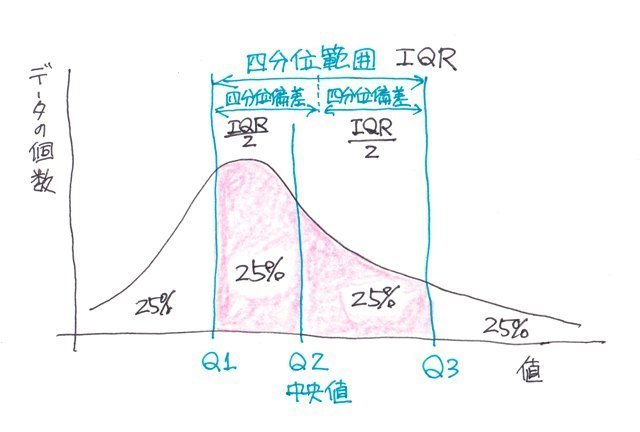
����͒����l�ɑΉ��������̑�\�l"�l���ʔ͈�"�A"�l���ʕ�"�ɂ��Đ������܂��傤�I
�o�b�N�i���o�[
1�D���ϒl�Ƒ�\�l�i�����l�j
2�D�Z�p���ρi�������ρj�Ɖ��d���ς̈Ⴂ�́H�u�d�݁v���ăi�j�I�H
�֘A�y�[�W
QUARTILE���Ŏl���ʓ_�����߂Ă݂�
���v���͂̊�{���̊�{�A�x�����z�\�ɂ��Ă܂Ƃ߂Ă݂�
���l�f�[�^�̕��z���݂�q�X�g�O�����ɂ��Ă܂Ƃ߂Ă݂�
���K���z�ɂ���
�����l�����߂�MEDIAN��
�f�[�^���͂̉��/���j���[

