NORMDIST(Normal cumulative distribution)関数を使用します。
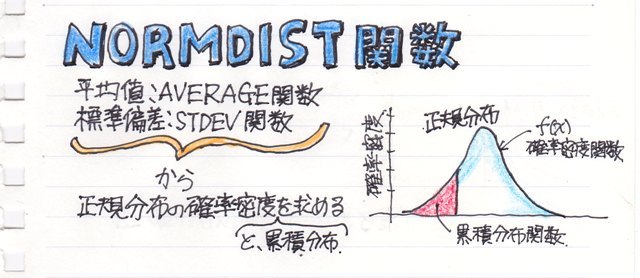
正規分布の基本的なことはまず、こちらをごらん下さい。。
んで、このような実際にデータ取りをした検査データがあります。基本的にこのデータは正規分布であると仮定します。
これから、平均値と標準偏差を求めて、それを元にNORMDIST関数で確率密度を求め正規分布のグラフを画いてみます。
また、累積分布を求めればデータの範囲にどのくらいの割合が含まれるか、含まれないかが推定できます。
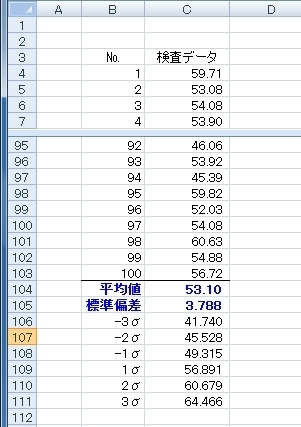
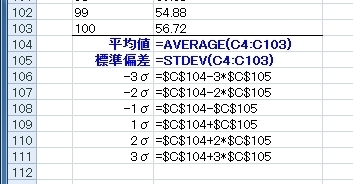
平均値は“AVERAGE関数”、標準偏差は“STDEV関数”を使って求めます。
それから、-3σ(平均値から標準偏差の3倍を引いた値)、-2σ、-1σ、1σ、2σ、3σ(平均値に標準偏差の3倍を足した値)も予め計算しておきました。
確率密度関数(正規分布)は平均値と標準偏差だけで求められますので、その時の“x値”(データ)は適当に-4σから4σぐらいの値を予め表に入れておきます。
そして、予め計算しておいた-3σから3σの値も表に入れ込んでおきます。
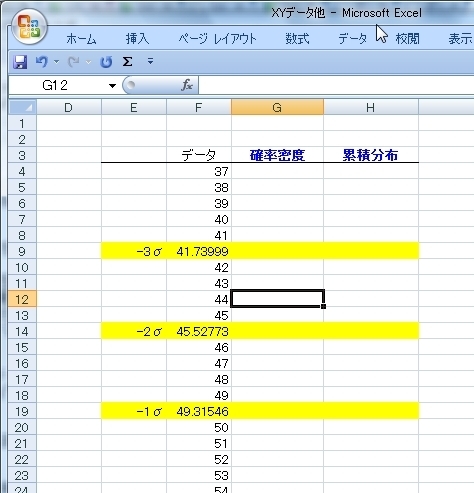
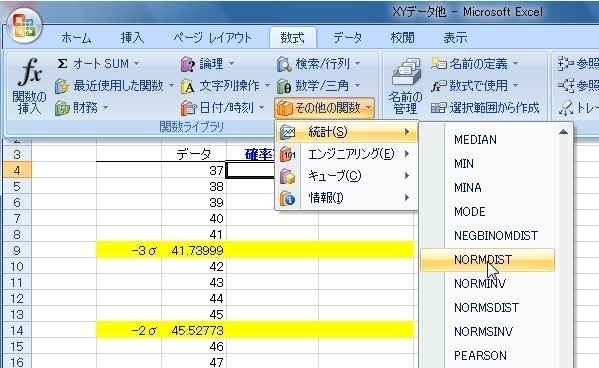
「数式」「その他の関数」「統計」から「NORMDIST」を選択します。
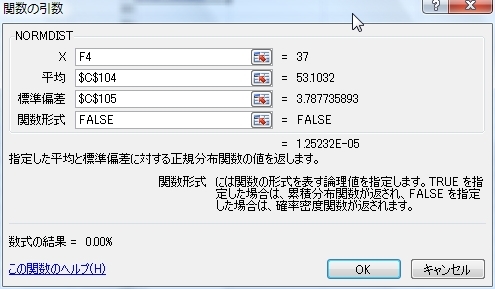
X:x値(データ)を指定します
平均:予め求めておいた平均値のセルを絶対位置($マーク付き)で指定します。
標準偏差:予め求めておいた標準偏差のセルを絶対位置($マーク付き)で指定します。
関数形式:ここで、“FALSE”にすると確率密度が求められます。
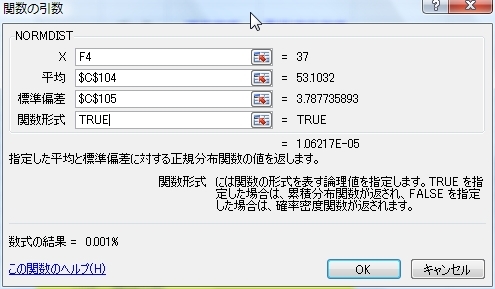
隣のセルには累積分布を求めます。
同様にNORMDIST関数で、“関数形式”は“TRUE”にします。
で、それを全ての行にコピーします。
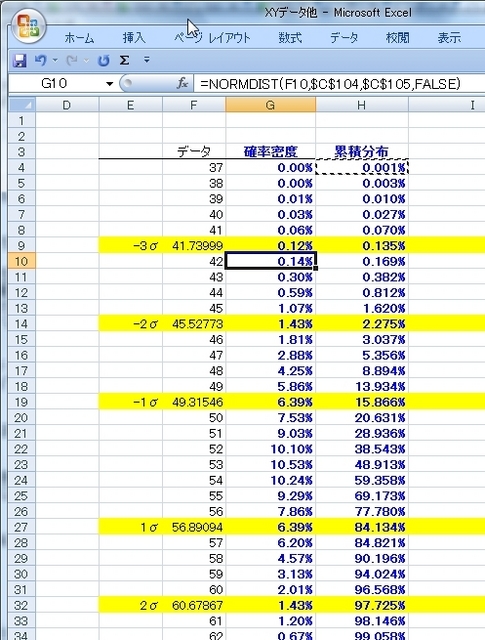
累積分布を見ると、-3σの時に“0.135%”になっています。これは、正規分布の解説にあった、「正規分布の範囲と推定」の値と一致していることが分かります。
この累積分布の値を使うことでデータの範囲の中にどれくらいの割合が含まれるかが推定できます。
例えば、-2σと3σのデータの範囲には“99.865%-2.275%=97.1%”のデータが含まれることが推定できます。
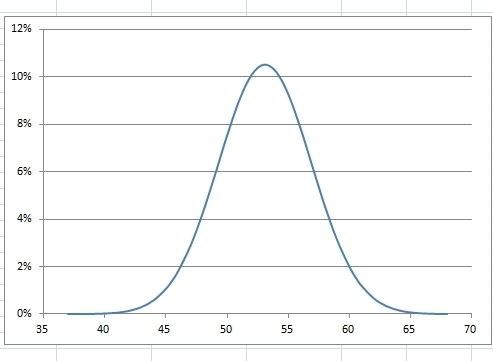
“x値(データ)”とNORMDISTの“確率密度”で散布図のグラフを作ると、平均値“53.10”、標準偏差“3.788”の正規分布のグラフが出来上がります。
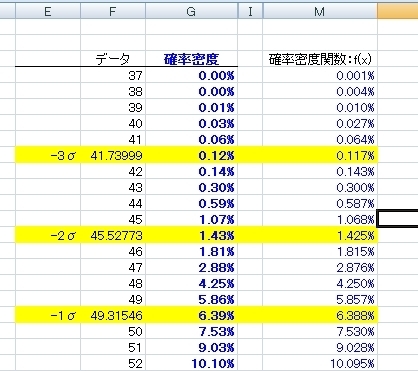
では、おまけに、正規分布の解説に出てきた確率密度関数の式で、手計算してみましょう。

式の中のかたまりを予め計算しておきます。
自然対数は“EXP関数”を使用しました。

すると、NOMDIST関数で求めた確率密度と一致していることが分かりましたね。。。
それから、ここでは説明のために「数式」の「関数ライブラリ」から関数を選択しましたが、あらかじめ関数が分かっている場合は式を入力するセルに直接“=NORMDIST()”と入力します。
“=N”と入力すると推定機能が働いて“N”で始まる関数が表示されるのでそこから選択することができます。
関連ページ
正規分布の解説
AVERAGE関数で平均値を求める
STDEV関数で標準偏差を求める
関数一覧(カテゴリ別)
関数一覧(名前別)
エラー値について(#VALUE!、#DIV/0!、#NAME?、#N/A、#REF!、#NUM!、#NULL!)

