直線で近似する場合
まずサンプルの元データを用意します。
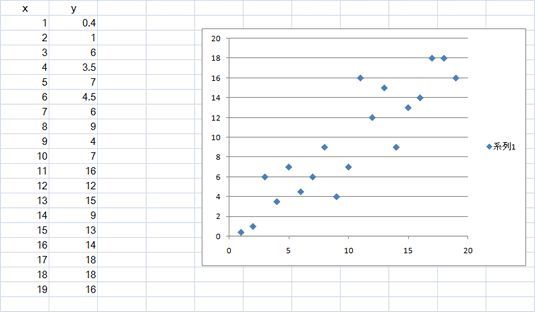
この様なX,Yのデータから最小二乗法を用いて直線で近似してみます。解りやすいようにグラフでも表示してみます。
このデータは y=xのデータ(直線)から、データを適当にばらつかせたものです。
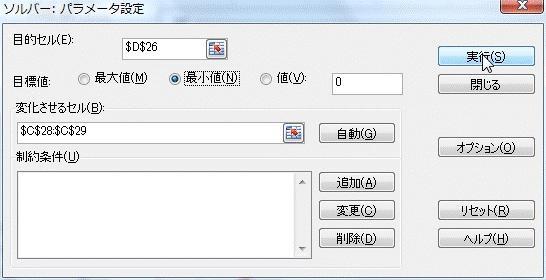
では直線の式 f(x)=ax+b の式を当てはめてみます。元々y=x ですから、a=1、b=0としてみます。
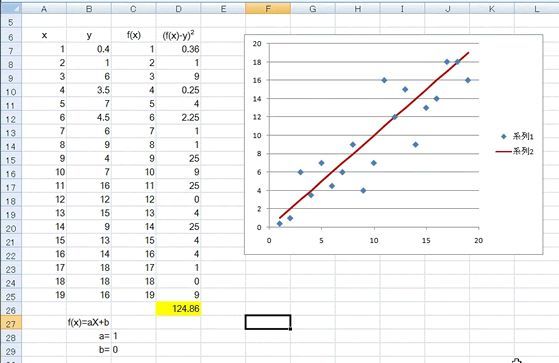
列Cに f(x)=ax+b (a=1,B=0) のデータを計算させています。計数aの値はC28、bの値はC29に入力し、f(x) の計算はそれらを引用して計算させます。(ソルバーではこの部分を最適化させます)
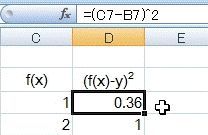
そして赤線でグラフを書いています。また列Dには(f(x)-y)^2のデータつまり残差の二乗を計算させています。(具体的には列Cの値から列Bの値を引いてから二乗しています)
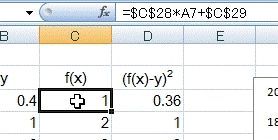
そして、27行目にその総和(合計)を算出しています。
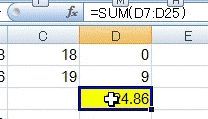
元々このデータからばらつかせたものですからこの赤い直線で十分近似しているようにもみえますが、残差の総和は"124.86"あります。
では早速、ソルバーを使って最小二乗法を実行してみましょう。
ソルバーの実行
まず、メニューの"データ"から"ソルバー"を選択します。ソルバーが表示されない場合は"オプション"の"アドイン"から、ソルバーを設定してください。
するとこのようなパラメータ設定画面が開きます。
ここでは、"目的セル"と"目標値"、"変化させるセル"を設定します。
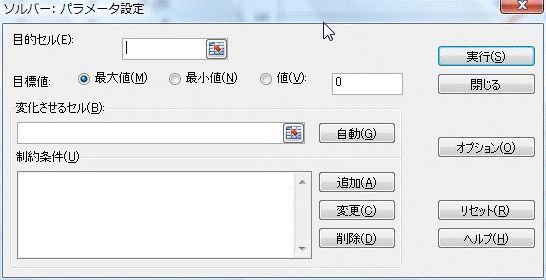
まず、"目的セル"は残差の総和のセルにします。
変化させるセルは、a,bの値のセルにします。
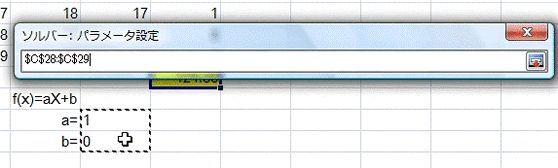
目標値を最小値(つまり残差の総和を小さくする)にして実行します。
すると、自動的にa,bの値が変わり、グラフも書き替りました。
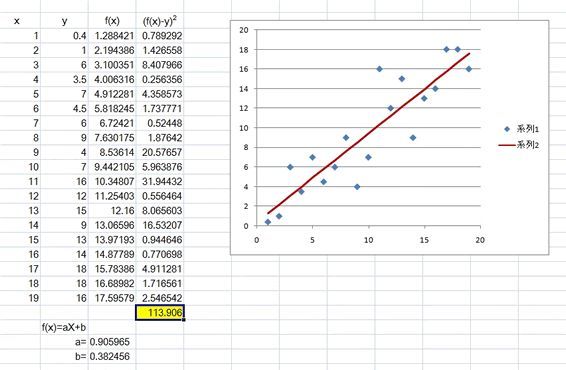
ソルバー実行後の画像aが0.905965、bが0.382456になり残差の総和は"113.906"となりました。
残差を更に小さくする
残差を小さくするとはどういうグラフになるでしょうか?
それは青いばらついている点それぞれに赤線が近づく曲線のグラフになります。つまりうねった曲線になります。
一般的に近似式の次数を大きくすると残差は少なくなります。先ほどのデータを3次式で近似してみます。
近似式は f(x)=ax^3+bx^2+cx+d とし、ソルバーを実行します。
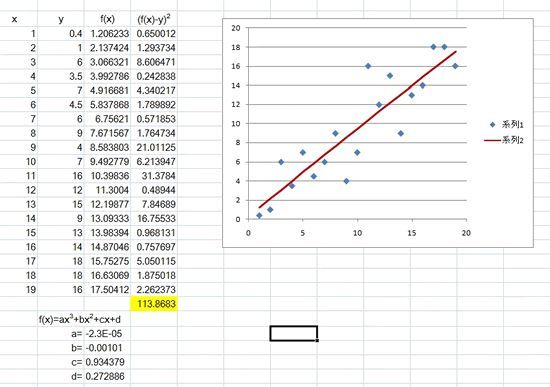
すると、このように赤いグラフが多少うねっています。残差の総和は"113.8683"となり、直線で近似した場合より小さくなりました。
この近似曲線は元のデータを近似してると言えるかどうか?単に残差を小さくするためにばらつきを拾っているとも言えます。
データを分析するために最小二乗法を使って近似式を推定する場合は、対象のデータがどのようなものか、何のために近似するかなどの条件によって適切な式f(x)を想定する必要があります。近似式f(x)の設定が間違っているとソルバーを使っても適切な近似は不可能です。
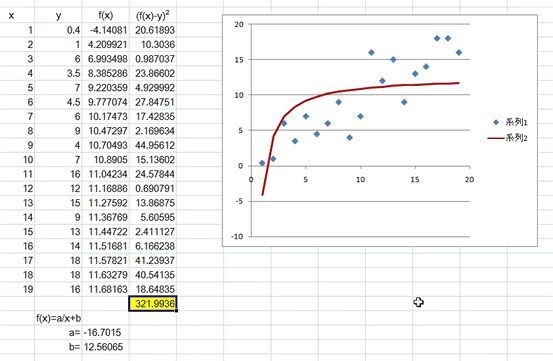
例えば、f(x)=a/x+b にしてしまうと。。。
こんなことになってしまいます。